Celsius to Fahrenheit Conversion: Complete Guide with Formulas [2025]
You're standing in a European airport, checking the weather forecast. It says 22°C. What does that actually mean in Fahrenheit? Or maybe you're cooking a recipe that calls for 180°C, but your oven only shows Fahrenheit. These everyday moments highlight why understanding temperature conversion isn't just academic—it's practical.
Temperature conversion between Celsius and Fahrenheit is one of those skills that seems simple on the surface but reveals fascinating complexity once you dig deeper. The two scales didn't emerge from the same thinking. They developed independently, rooted in different historical contexts and scientific frameworks. Understanding why they exist, how they relate, and how to convert between them gives you insight into how measurement systems evolve and why precision matters.
In this comprehensive guide, we'll walk through everything you need to know about converting Celsius to Fahrenheit. You'll learn the mathematical foundation, work through solved examples, discover practical applications, and understand the historical context behind these temperature scales. By the end, you won't just know the formula—you'll understand why it works and when you actually need to use it.
TL; DR
- The conversion formula is simple: °F = (°C × 9/5) + 32 or °F = (°C × 1.8) + 32
- Water freezes at 0°C (32°F) and boils at 100°C (212°F), creating a 180°F span vs. 100°C
- The ratio 9/5 exists because Celsius divides the freezing-to-boiling range into 100 degrees while Fahrenheit uses 180 degrees
- Quick mental math: Double the Celsius number, subtract 10%, and add 32 for a rough approximation
- Room temperature is approximately 20-22°C, which equals 68-72°F, a comfortable baseline for remembering the scales
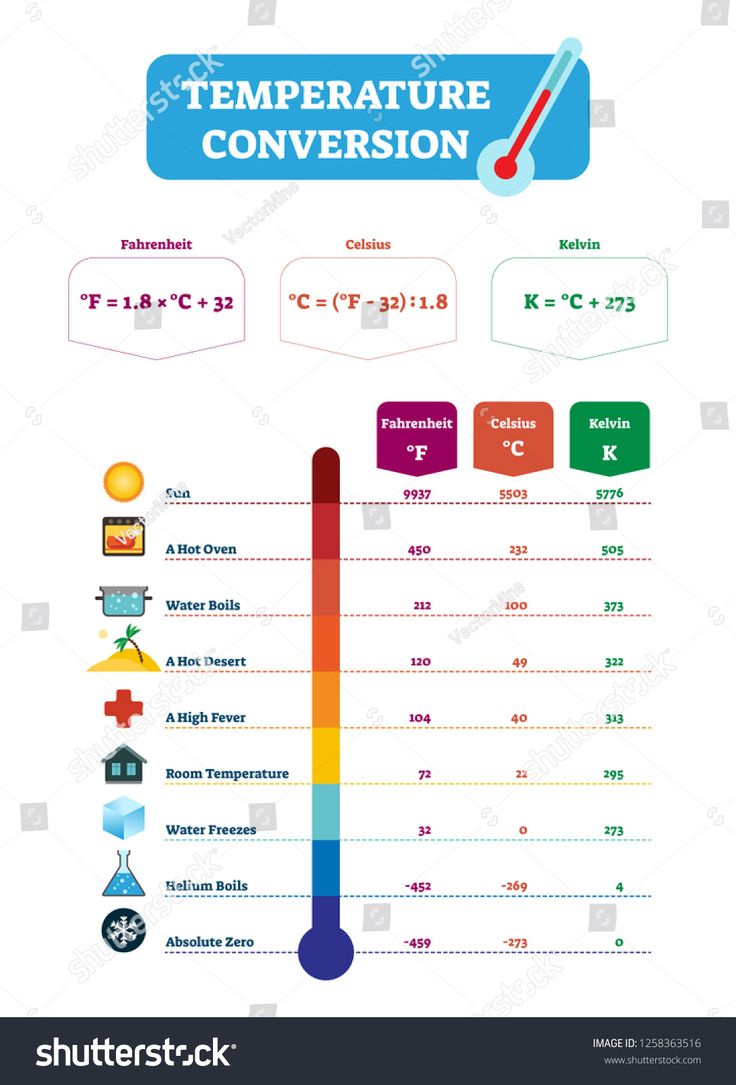
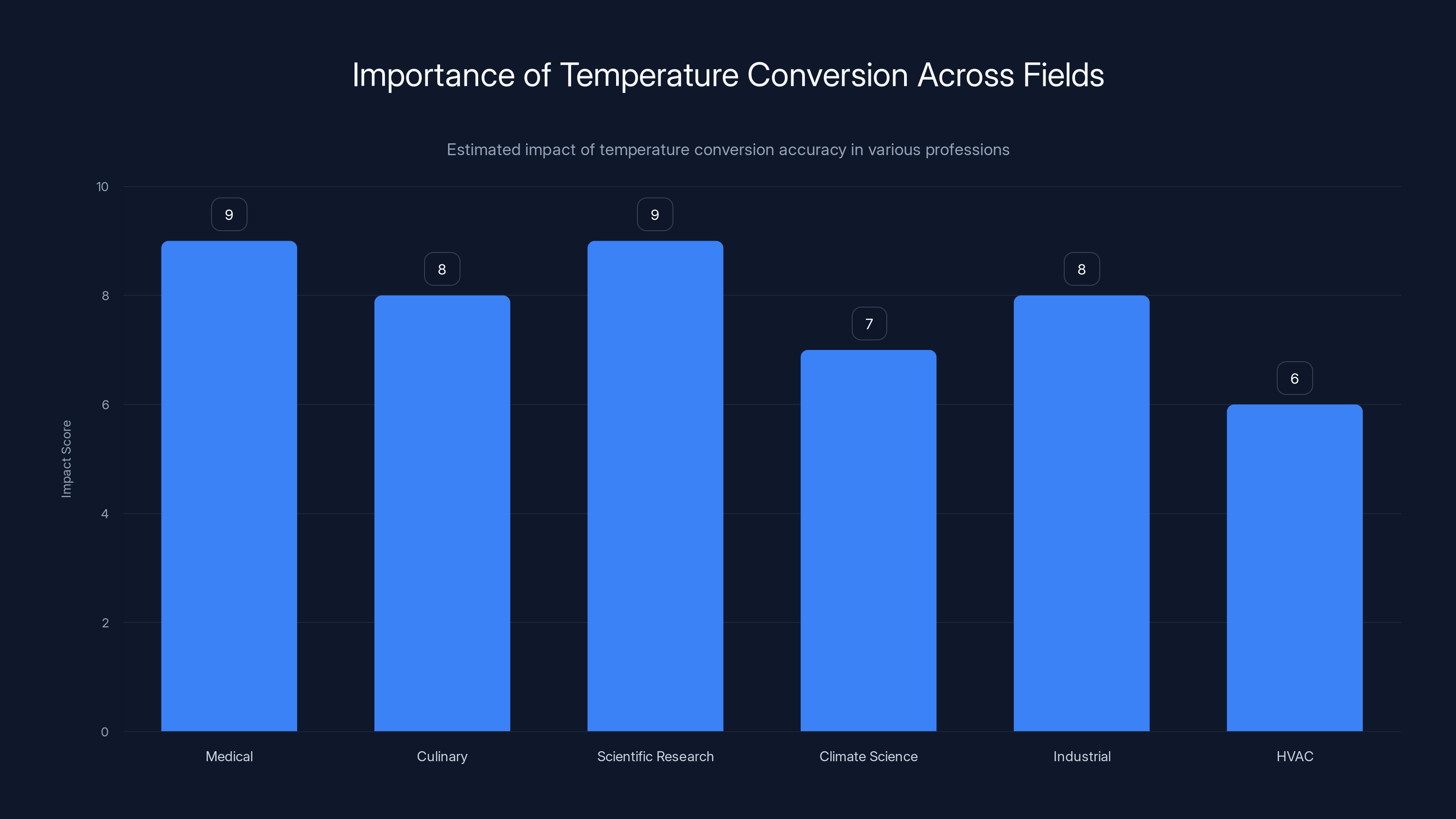
Temperature conversion accuracy is crucial across various fields, with medical and scientific research scoring highest in impact. Estimated data.
Understanding Temperature Scales: The Fundamentals
Before jumping into conversion, it's worth understanding what temperature actually measures and why we have multiple ways to express it. Temperature represents the kinetic energy of molecules—essentially, how much they're moving around. But how we measure and quantify that motion is entirely arbitrary. We invented the numbers. We chose the reference points. This is where Celsius and Fahrenheit diverge.
The Celsius Scale Explained
Celsius emerged from Swedish astronomer Anders Celsius in 1742. His scale was elegantly simple: pick two universally observable phenomena, assign them fixed points, and divide the space between them into equal intervals. Water freezes at 0°C. Water boils at 100°C. The space between them? Divided into exactly 100 equal degrees.
This is why Celsius dominates scientific work. Scientists love systems based on round numbers and universal constants. The metric system itself grew from similar thinking—base-10 everything, simple, rational. A chemist in Tokyo and another in São Paulo can communicate temperature values without confusion because the scale is standardized globally.
When meteorologists say it's 20°C outside, they're saying it's one-fifth of the way from water's freezing point to its boiling point. When a recipe requires 180°C, that's nearly to boiling point but not quite—around 90% of the way up the scale.
The Fahrenheit Scale Explained
Fahrenheit came later, developed by Daniel Fahrenheit in 1714. His approach was different. Instead of using water's freezing point as zero, he chose a salt-and-ice mixture's freezing point as zero. His boiling point for water? 212°F. This created 180 degrees between freezing and boiling—a less intuitive choice, but one rooted in his thinking about brine solutions and practical thermometry.
What's crucial to understand: Fahrenheit wasn't designed to be illogical. It was designed with different reference points. It offered finer granularity—180 degrees instead of 100—which some argued was useful for precision in everyday temperatures. A degree Fahrenheit is smaller than a degree Celsius, so incremental changes feel more significant.
The United States, the Bahamas, Belize, the Cayman Islands, and a handful of other territories still use Fahrenheit. Everyone else uses Celsius. This isn't because one is objectively better—it's because of historical adoption and the global dominance of the metric system, which includes Celsius.
Why The Numbers Don't Align
Here's something that confuses many people: Celsius and Fahrenheit don't have a simple, clean relationship like miles to kilometers (which is 1:1.609). Instead, you have this awkward fraction: 9/5 or 1.8.
Why? Because the ratio of degrees is mathematically determined by the reference points.
- Celsius range: 0°C to 100°C = 100 degree intervals
- Fahrenheit range: 32°F to 212°F = 180 degree intervals
- Ratio: 180 ÷ 100 = 1.8 or 9/5
That's it. The 9/5 relationship emerges directly from how the scales were constructed. It's not random—it's inevitable math.
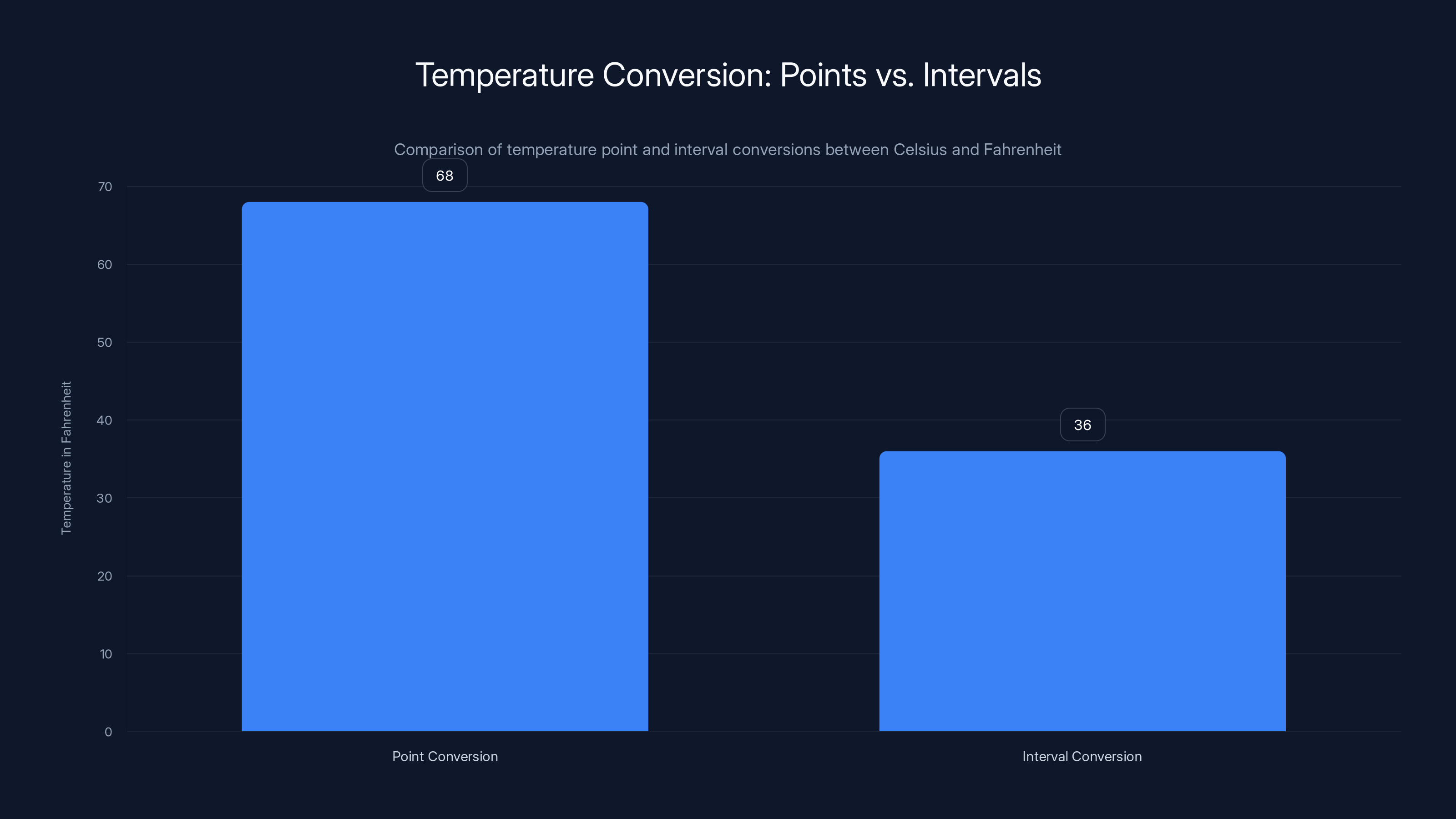
Temperature point conversion from 20°C results in 68°F, while a 20°C interval results in a 36°F increase. This distinction is crucial in scientific contexts.
The Complete Conversion Formula
Now let's get into the mathematical mechanics. The formula is straightforward, but understanding each component deepens your grasp of why it works.
The Primary Conversion Formula
The standard formula for converting Celsius to Fahrenheit is:
Or equivalently:
Both are identical. The first uses the fractional form (9/5), which some prefer because it shows the mathematical origin. The second uses the decimal (1.8), which is easier for quick mental math.
Breaking Down Each Component
Let's dissect what's happening here:
Step 1: Multiply by 9/5 (or 1.8)
This converts the Celsius interval to a Fahrenheit interval. Remember, 100 Celsius degrees equals 180 Fahrenheit degrees. So one Celsius degree equals 1.8 Fahrenheit degrees. If you have a temperature change of 10°C, that's a change of 18°F.
Step 2: Add 32
This accounts for the offset between the scales. Celsius starts at 0 (water's freezing point), but Fahrenheit starts at 32 for the same phenomenon. So every Celsius temperature needs 32 added to align the reference points.
Why Not Subtract or Use Different Numbers?
You might wonder if there's an alternative formula. There isn't—not mathematically. Any temperature conversion must:
- Account for the scale ratio (9/5)
- Account for the reference point offset (32)
Try this yourself: If 0°C = 32°F and 100°C = 212°F, the only formula that satisfies both conditions is °F = (°C × 9/5) + 32. Math doesn't allow alternatives.
Reverse Conversion (Fahrenheit to Celsius)
For completeness, the reverse formula is:
Notice the operations reverse: subtract 32 first (remove the offset), then multiply by 5/9 (convert the scale ratio). The order matters here because of how algebra works.
Step-by-Step Conversion Process
Now let's apply the formula systematically. Having a process removes confusion and ensures accuracy.
Process for Converting Any Celsius Temperature
Step 1: Write down the Celsius temperature
Example: 25°C
Step 2: Multiply the number by 9/5
25 × 9/5 = 25 × 1.8 = 45
Step 3: Add 32
45 + 32 = 77
Step 4: Write the result with the Fahrenheit symbol
25°C = 77°F
Step 5: Verify with context
Does 77°F make sense for 25°C? That's room temperature, warm but not hot. Yes, that aligns.
Handling Negative Temperatures
The process doesn't change, but working with negative numbers requires care.
Example: -10°C to Fahrenheit
(-10) × 1.8 = -18
-18 + 32 = 14
So -10°C = 14°F (quite cold, below freezing)
Notice: even though we're multiplying a negative number, the process is identical. The math handles it naturally.
Decimal Temperatures
Sometimes you'll encounter temperatures like 37.5°C. The process remains exactly the same.
37.5 × 1.8 = 67.5
67.5 + 32 = 99.5°F
Decimal precision carries through naturally.
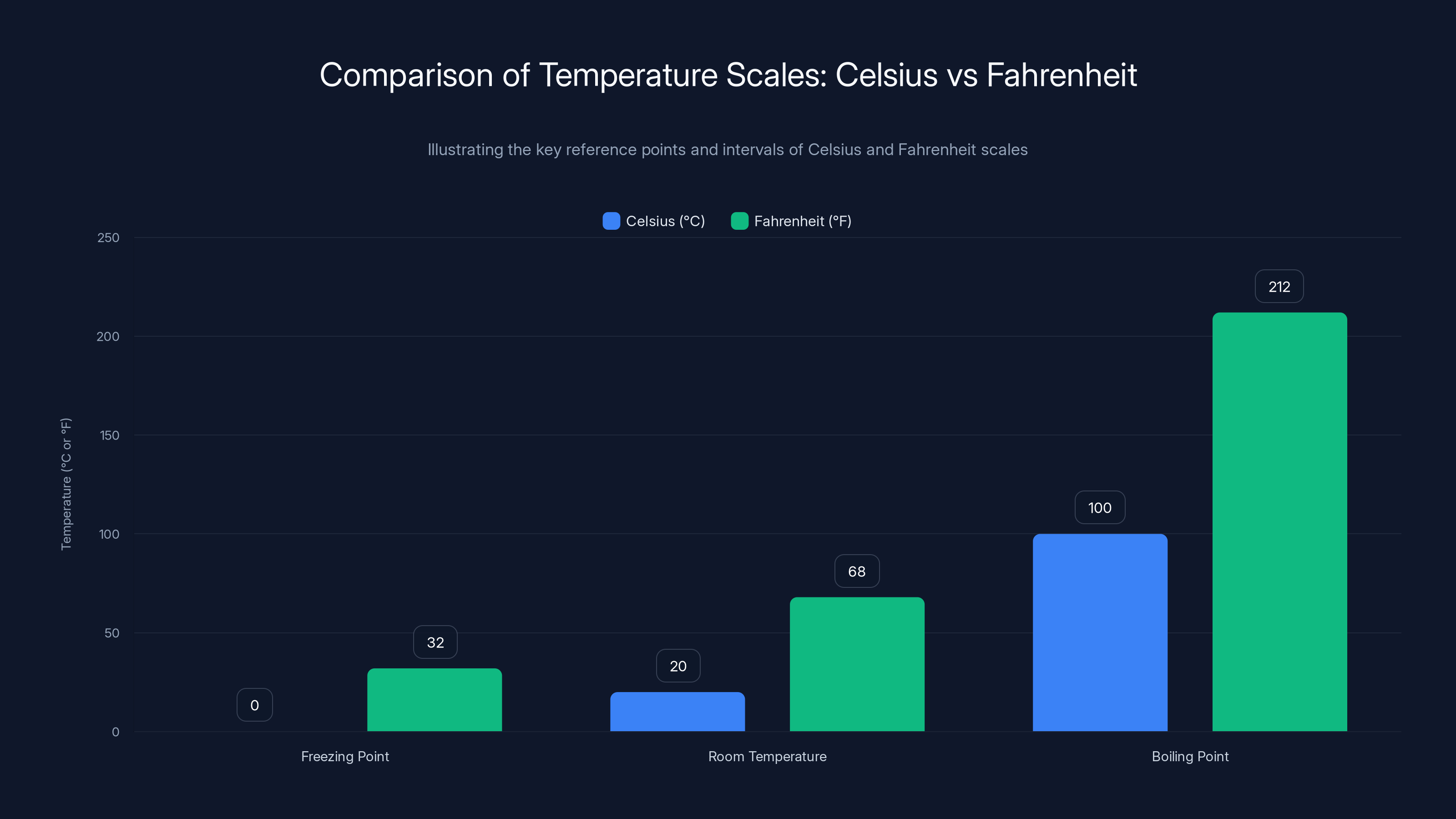
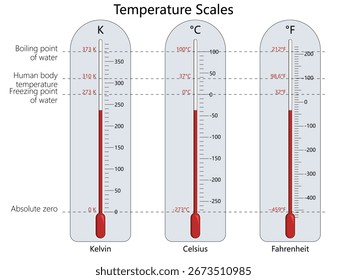
This chart compares Celsius and Fahrenheit scales at key reference points: freezing, room temperature, and boiling. Celsius uses a 100-degree interval between freezing and boiling, while Fahrenheit uses 180 degrees.
Real-World Solved Examples
Let's work through practical scenarios where you'd actually need this conversion.
Example 1: International Travel (Planning What to Wear)
Scenario: You're visiting Barcelona, and the weather forecast says 28°C. You want to know if you need a jacket.
Given: 28°C
Solution:
°F = (28 × 1.8) + 32
°F = 50.4 + 32
°F = 82.4°F
Result: 82.4°F is warm and sunny. No jacket needed. Perfect for short sleeves or light clothing.
Example 2: Cooking and Baking
Scenario: A European recipe calls for baking at 180°C, but your American oven shows Fahrenheit only.
Given: 180°C
Solution:
°F = (180 × 1.8) + 32
°F = 324 + 32
°F = 356°F
Result: Set your oven to 356°F (most ovens round this to 350°F or 360°F for practical purposes).
Example 3: Body Temperature and Fever
Scenario: Your child has a temperature of 38.5°C. You need to communicate this to an American pediatrician who works in Fahrenheit.
Given: 38.5°C
Solution:
°F = (38.5 × 1.8) + 32
°F = 69.3 + 32
°F = 101.3°F
Result: 101.3°F indicates a moderate fever (normal is around 98.6°F). Medical action might be warranted depending on other symptoms.
Example 4: Scientific Experiment
Scenario: A chemistry lab reports that a reaction occurs at -15°C. You need this in Fahrenheit for a research paper.
Given: -15°C
Solution:
°F = (-15 × 1.8) + 32
°F = -27 + 32
°F = 5°F
Result: 5°F is well below freezing, indicating a very cold reaction environment. This might require specialized equipment.
Example 5: Climate and Weather Extremes
Scenario: Death Valley recorded 54°C, one of the hottest temperatures on Earth. What is this in Fahrenheit?
Given: 54°C
Solution:
°F = (54 × 1.8) + 32
°F = 97.2 + 32
°F = 129.2°F
Result: 129.2°F is dangerously hot. At this temperature, exposed skin can blister in minutes. This explains why Death Valley is considered one of the hottest places on the planet.
Comprehensive Conversion Reference Table
Sometimes you just need to look something up. Here's a practical reference for common temperatures:
| Celsius (°C) | Fahrenheit (°F) | Context/Usage |
|---|---|---|
| -40 | -40 | Crossover point where both scales match |
| -30 | -22 | Extremely cold; dangerous without protection |
| -20 | -4 | Deep winter in cold climates |
| -10 | 14 | Freezing cold; snow likely |
| 0 | 32 | Water freezes; reference point |
| 5 | 41 | Just above freezing; cold winter day |
| 10 | 50 | Cool but manageable; light jacket |
| 15 | 59 | Spring weather; sweater appropriate |
| 20 | 68 | Room temperature; comfortable |
| 22 | 72 | Ideal indoor temperature |
| 25 | 77 | Warm; summer day |
| 30 | 86 | Hot; air conditioning appreciated |
| 35 | 95 | Very hot; stay hydrated |
| 37 | 98.6 | Normal human body temperature |
| 40 | 104 | Extreme heat; heat advisory |
| 50 | 122 | Dangerous heat; limit outdoor activity |
| 100 | 212 | Water boils; reference point |
This table gives you anchoring points. If you know 20°C is room temperature and comfortable, you can estimate nearby temperatures by comparison.
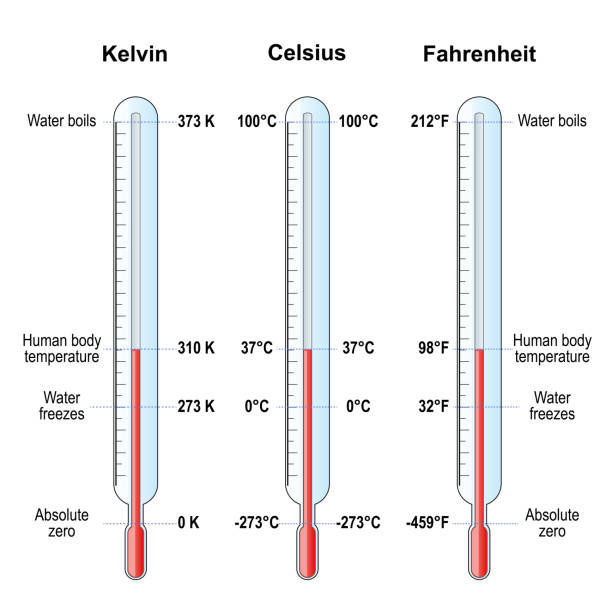
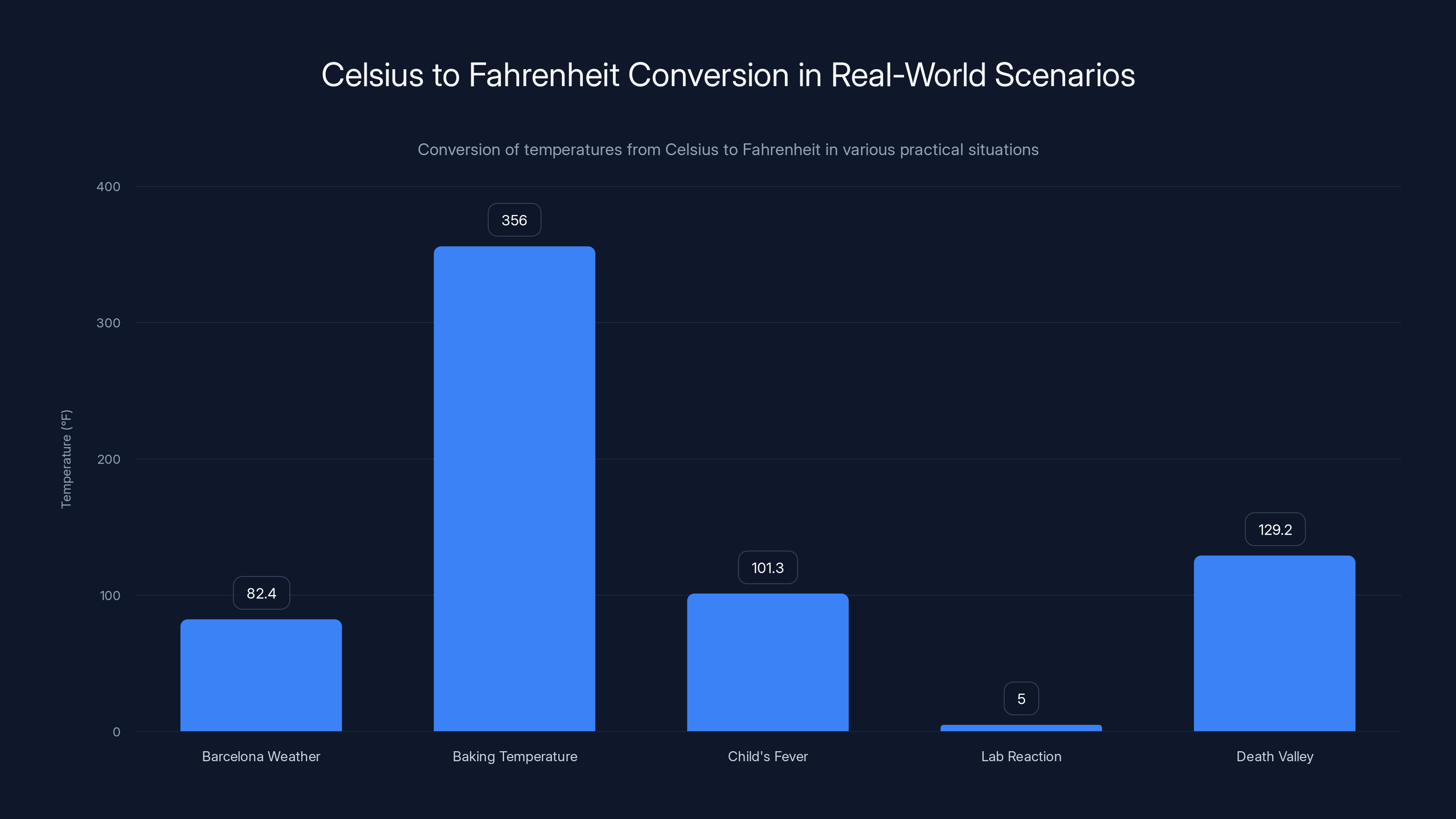
This bar chart illustrates the conversion of temperatures from Celsius to Fahrenheit across five real-world scenarios, highlighting the practical application of temperature conversion.
The Historical Development of Temperature Scales
Understanding history provides context for why these scales exist. It's not just abstract science—it's how humans solved measurement problems with the tools available.
Before Standardized Scales
Before Celsius and Fahrenheit, people used crude descriptions: hot, cold, warm, freezing. When precision mattered, like in medicine or alchemy, people used thermoscopes (devices that showed temperature change but didn't measure it numerically). These devices had no standardized scale, so one person's "very hot" wasn't another's "very hot."
Trade suffered. Science stagnated. Recipes varied. Medicines were inconsistent.
Fahrenheit's Innovation (1714)
Daniel Fahrenheit, a German physicist and instrument maker, created the first reliable mercury thermometer and developed a scale to go with it. He chose three reference points:
- Zero: salt-water ice mixture (the coldest he could reliably produce)
- Mid-point: human body temperature (approximately 96°F in his scale)
- Boiling point: water boiling (212°F)
Fahrenheit's scale had practical advantages for his era. The 180 divisions between freezing and boiling meant temperatures could be expressed as whole numbers more often. This mattered when handwriting measurements—fewer fractions.
Celsius's Simplicity (1742)
Swedish astronomer Anders Celsius proposed a decimal-based alternative. He kept Fahrenheit's thermometer principle but used only two reference points:
- Zero: water's freezing point
- 100: water's boiling point
Celsius's scale aligned with emerging decimal thinking. As the metric system developed (especially after the French Revolution), Celsius became the obvious choice for standardization. It was rational, base-10, scientifically motivated, and international.
Kelvin's Absolute Scale (1848)
William Thomson, later Lord Kelvin, made a crucial observation: you can't have a temperature below absolute zero. Mathematically, there's a lower limit where molecular motion stops entirely. This occurs at -273.15°C.
Kelvin proposed a new scale starting at absolute zero: zero Kelvin equals -273.15°C. Scientists adopted this immediately for research because Kelvin temperatures never require negative numbers and scale linearly with molecular energy.
Why Fahrenheit Persists in America
Fahrenheit didn't disappear because of historical inertia. The United States adopted Fahrenheit early, built infrastructure around it, and made the switch to metric politically difficult. Attempts to metricate the US in the 1970s faced public resistance, partly because temperature was such a culturally ingrained part of daily life.
Even today, Americans know room temperature is 72°F, body temperature is 98.6°F, and water boils at 212°F. These numbers are embedded in daily understanding. Celsius would require relearning—70 degrees would feel cold, 35 degrees would mean "death freeze," and 100 degrees would seem barely boiling.
Common Temperature Benchmarks Across Both Scales
Memory anchors help you internalize these scales. Knowing key reference points makes estimation intuitive.
Everyday Temperatures
Cold Environments:
- -20°C (-4°F): Deep winter, dangerous without proper clothing
- -10°C (14°F): Freezing cold, typical harsh winter
- 0°C (32°F): Freezing point of water, snow and ice common
- 5°C (41°F): Just above freezing, winter in mild climates
Comfortable Temperatures:
- 15°C (59°F): Cool but tolerable, light jacket
- 20°C (68°F): Room temperature, comfortable indoors
- 22°C (72°F): Often considered ideal indoor temperature
- 25°C (77°F): Warm, summer weather
Hot Environments:
- 30°C (86°F): Hot, summer heat, sweating
- 35°C (95°F): Very hot, heat advisories issued
- 40°C (104°F): Extreme heat, dangerous outdoors
- 50°C (122°F): Death Valley heat, survive-only temperatures
Biological Reference Points
Human Body:
- Normal body temperature: 37°C (98.6°F)
- Mild fever: 38-39°C (100-102°F)
- Serious fever: 40°C+ (104°F+)
The normal body temperature benchmark is useful: if you're uncomfortable and someone mentions a 40°C fever, that's roughly 3°C above normal—about 5.4°F—indicating a significant infection.
Water Phase Changes
- Freezing point: 0°C (32°F)
- Boiling point: 100°C (212°F)
- Ice cream soft point: -10°C (14°F)
- Steam formation: just above 100°C
These reference points are universal and appear in countless contexts, from cooking to medicine to climate science.
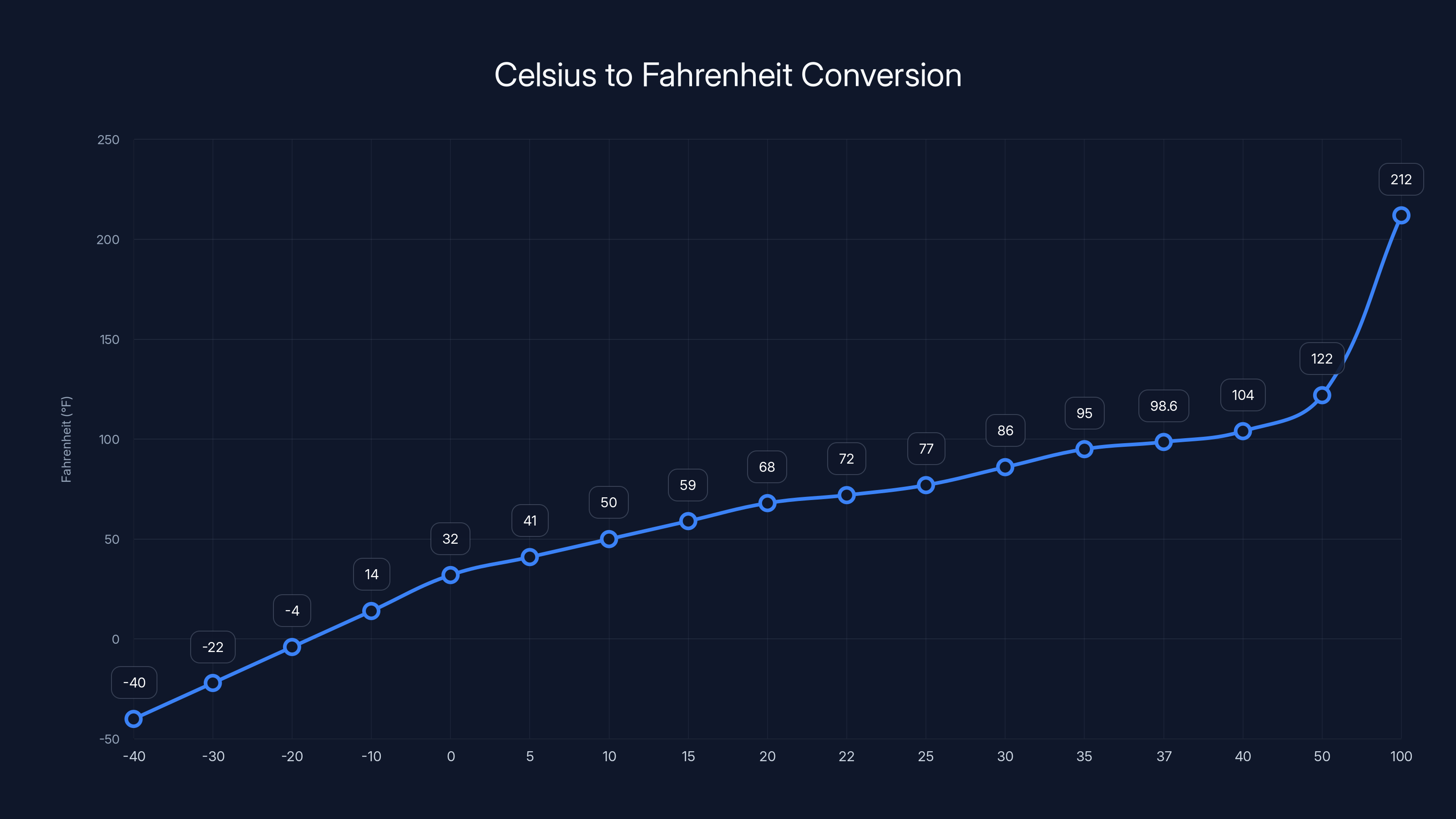
This line chart illustrates the conversion of temperatures from Celsius to Fahrenheit, highlighting key temperature points such as freezing, room temperature, and boiling.
Why the Conversion Formula Matters in Different Fields
Temperature conversion isn't just academic. It's mission-critical in specific professions.
Medical and Healthcare Applications
Doctors and nurses in different countries need instant, accurate conversions. A child's fever of 39°C needs to communicate as 102.2°F in America or vice versa. Medication dosages and treatment protocols sometimes depend on precise temperature readings.
Additionally, different countries use different thermometers and temperature measurement equipment. Understanding the conversion ensures safety and prevents medical errors.
Culinary Arts
Recipes travel globally. A French pastry recipe might specify 165°C, while an American cookbook uses 325°F. Professional bakers must convert accurately—pastry baking is science, not art. A 10-degree error can ruin the entire batch.
Oven temperature directly affects:
- Crust color and texture
- Interior cooking speed
- Moisture retention
- Rising of baked goods
Scientific Research and Laboratories
Most global science uses Celsius for data collection and Kelvin for calculations. American researchers must convert between Celsius and Fahrenheit when publishing in certain journals or collaborating internationally. Accuracy is paramount because experimental precision depends on it.
Climate Science and Meteorology
Weather forecasters and climate scientists predominantly use Celsius, but must communicate with American audiences in Fahrenheit. Climate change discussions involve precise temperature shifts (like 1.5°C warming), which lose meaning if converted carelessly.
Industrial and Manufacturing
Manufacturing processes often specify exact temperatures. A steel tempering process might require 650°C, while an American facility has equipment calibrated in Fahrenheit. Getting this wrong can destroy expensive materials or create defective products.
HVAC and Climate Control
Building heating and cooling systems must maintain specified temperatures. International companies with facilities worldwide need staff trained in both systems to avoid costly mistakes.
Quick Mental Approximation Techniques
Sometimes you need a ballpark estimate without perfect accuracy. These mental math tricks are surprisingly useful.
Method 1: Double and Add 30
For quick approximations:
°F ≈ (°C × 2) + 30
This isn't perfect but gets you close:
- 0°C: (0 × 2) + 30 = 30°F (actual: 32°F) — off by 2
- 10°C: (10 × 2) + 30 = 50°F (actual: 50°F) — perfect
- 20°C: (20 × 2) + 30 = 70°F (actual: 68°F) — off by 2
- 30°C: (30 × 2) + 30 = 90°F (actual: 86°F) — off by 4
This works best in the 10-30°C range, which covers most daily temperatures.
Method 2: Subtract 30 and Divide by 2 (Fahrenheit to Celsius)
Going the other direction:
°C ≈ (°F - 30) / 2
Examples:
- 32°F: (32 - 30) / 2 = 1°C (actual: 0°C) — very close
- 50°F: (50 - 30) / 2 = 10°C (actual: 10°C) — perfect
- 68°F: (68 - 30) / 2 = 19°C (actual: 20°C) — off by 1
- 86°F: (86 - 30) / 2 = 28°C (actual: 30°C) — off by 2
Again, the 32-86°F range gives best results.
Method 3: Use the 10-Degree Rule
For rough estimates, remember that 1°C ≈ 1.8°F, so roughly 10°C ≈ 18°F.
If you know 20°C is 68°F, then:
- 30°C would be roughly 68 + 18 = 86°F (actual: 86°F) — perfect
- 10°C would be roughly 68 - 18 = 50°F (actual: 50°F) — perfect
This proportional thinking works well when you have a known anchor point.
Method 4: The Precise Calculation (When You Need Accuracy)
When approximation isn't sufficient, use the full formula:
Break it into steps if needed:
- Multiply by 1.8
- Add 32
With a calculator, this takes 20 seconds. There's no faster way to get exact results.
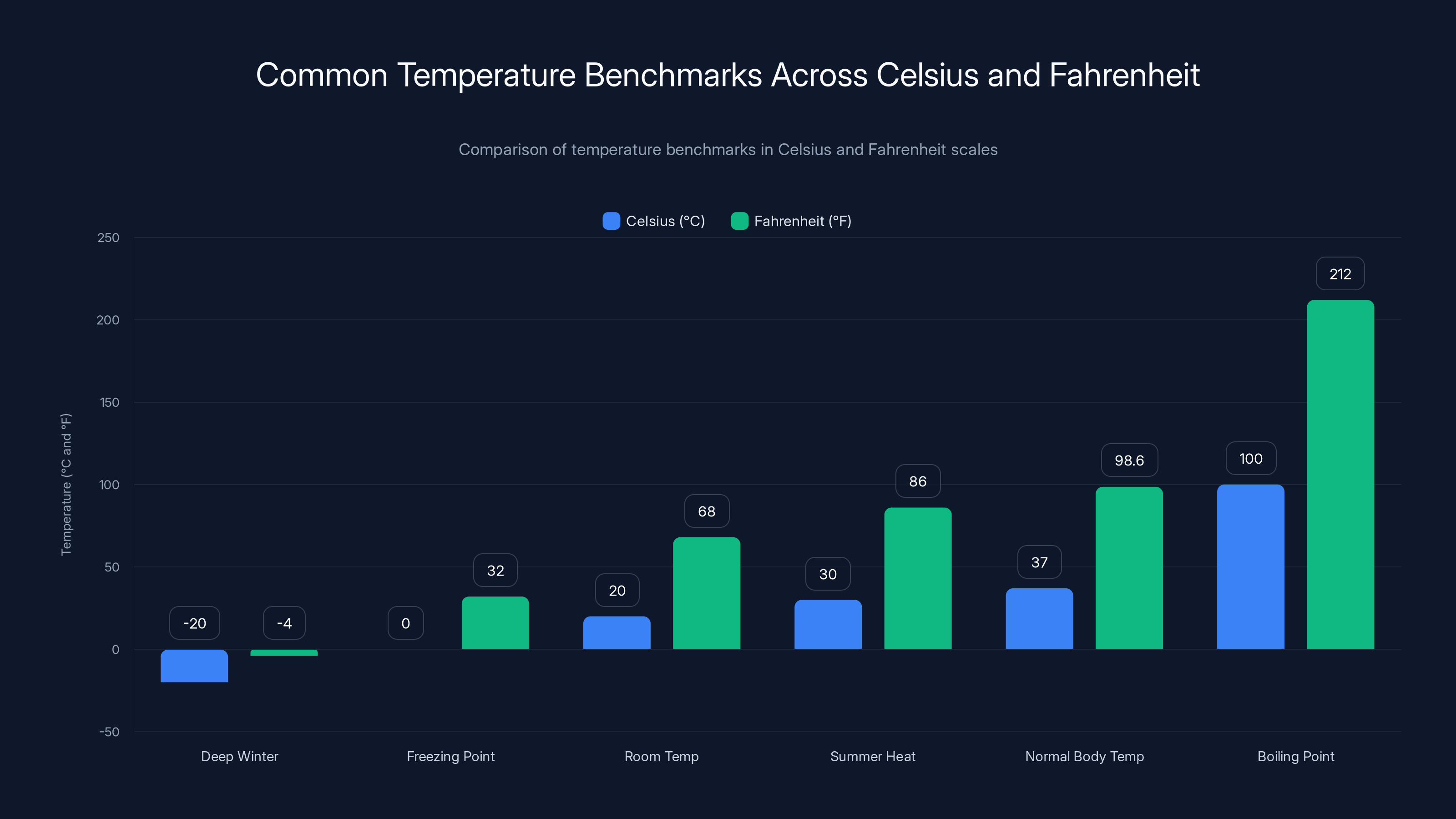
This chart illustrates key temperature benchmarks across both Celsius and Fahrenheit scales, highlighting common environmental and biological reference points.
Common Mistakes in Temperature Conversion
People make predictable errors. Here's how to avoid them.
Mistake 1: Forgetting to Add 32
Wrong approach: 25°C × 1.8 = 45°F
Correct approach: (25 × 1.8) + 32 = 77°F
The +32 is absolutely critical. It accounts for the offset between reference points. Skipping it is a massive error.
Mistake 2: Reversing the Order in Fahrenheit-to-Celsius Conversion
Wrong approach: (50 - 32) ÷ 1.8 gives wrong result if you divide first instead of subtracting
Correct approach: (50 - 32) ÷ 1.8 = 18 ÷ 1.8 = 10°C
The order matters. Algebra demands: subtract the offset first, then scale.
Mistake 3: Confusing 9/5 and 5/9
Wrong approach: Using 5/9 when converting Celsius to Fahrenheit
Correct approach: Use 9/5 for Celsius→Fahrenheit, and 5/9 for Fahrenheit→Celsius
Remember: 9/5 is greater than 1 (equals 1.8), so Fahrenheit temperatures are always larger in magnitude than their Celsius equivalents (except at -40). This can help you check your work.
Mistake 4: Sloppy Decimal Handling
Wrong approach: 37.5°C × 1.8 = 67.5, but then rounding to 68 and adding 32 = 100°F
Correct approach: 37.5 × 1.8 = 67.5, then 67.5 + 32 = 99.5°F
Round only at the very end, after all calculations. Rounding midway introduces cumulative error.
Mistake 5: Assuming the Conversion is Linear Beyond the Freezing-Boiling Range
Conceptual error: Thinking the formula somehow changes for temperatures outside typical ranges
Reality: The formula works identically for -100°C, 0°C, 50°C, or 1000°C. The math doesn't care. Temperature conversion is linear—it works the same everywhere on the scale.

Advanced Concepts: Beyond Simple Conversion
For those interested in deeper understanding, there are fascinating extensions of temperature conversion.
Absolute Temperature Scales
Celsius and Fahrenheit are arbitrary—they have negative numbers because the scales don't start at zero energy. But absolute temperature scales start at absolute zero, where molecular motion ceases entirely.
Kelvin scale (used by scientists):
K = °C + 273.15
Rankine scale (absolute version of Fahrenheit, rarely used):
°R = °F + 459.67
Kevin is how scientists think about temperature because it's proportional to molecular kinetic energy. If you double the Kelvin temperature, you've double the average molecular speed.
Temperature Intervals vs. Temperature Points
Here's a subtle distinction that matters in science:
- Temperature point: An absolute measurement (20°C is a specific point)
- Temperature interval: A difference or change (20°C change is an interval)
Intervals convert differently than points:
- Point: 20°C = 68°F (using the full formula)
- Interval: A 20°C increase = a 36°F increase (only multiply by 9/5, no +32)
This matters in scientific contexts where you're measuring change, not absolute values.
Thermal Equilibrium and Temperature Scales
Why do we need temperature scales at all? Because they quantify thermal equilibrium—when two objects placed together stop exchanging heat, they've reached the same temperature. The scale is just our way of numbering this equilibrium state.
Practical Precision Considerations
While the formula is mathematically exact, real-world thermometers have limited precision. A typical thermometer reads to the nearest 0.1°C or 0.5°F. Reporting a conversion as 77.34°F when your source is 25°C implies false precision—your source was probably known to only ±0.5°C anyway.
In professional contexts, always consider the precision of your measurements and don't over-report precision in conversions.
Practical Applications in Everyday Life
These conversions aren't abstract. They touch your daily life in concrete ways.
Travel Planning
When planning international travel, weather forecasts are your first check. European forecasts use Celsius; American ones use Fahrenheit. Quick conversions let you pack appropriately.
Example: "London shows 15°C." You calculate: 15 × 1.8 + 32 = 59°F. That's cool—a sweater and light jacket.
Without this conversion, you might pack for warm weather and arrive underdressed.
Cooking and Baking
Recipe sources are geographically mixed. A French baking blog specifies 200°C; an American cookbook specifies 400°F. Quick conversion ensures you're using the right temperature.
For baking especially, precision matters. A 25-degree error can affect rising, browning, and texture.
Health and Illness
Parenting often requires converting a child's fever temperature for a doctor's appointment or to communicate with family in another country. A temperature of 38.5°C needs to be communicated as 101.3°F in some contexts.
Home Heating and Cooling
If you move internationally or buy smart home equipment from another country, thermostats might display the "wrong" temperature scale. Converting quickly prevents accidentally setting your heat to an unreasonable value.
Car Maintenance
Car maintenance specs and engine operating temperatures are sometimes listed in different scales depending on manufacturer origin. Proper maintenance requires accurate readings.
Swimming and Water Safety
Water temperature affects swimming safety. A pool at 20°C (68°F) feels cold; at 27°C (80°F) feels comfortable; at 40°C (104°F) would be dangerously hot (and actually scalding). Quick conversions help you understand water safety implications.
Technology and Tools for Temperature Conversion
While understanding the formula is important, technology makes conversions easier.
Calculator Approach
Simple and reliable. Enter: (Celsius × 1.8) + 32. Most phones have calculators. Takes 30 seconds.
Online Conversion Tools
Websites like Convert Units.com or specialized temperature calculators instantly convert. These are accurate and take seconds.
Smartphone Apps
Many weather apps automatically show both scales. Unit converter apps (like Unit Converter, Convertinator) handle temperature alongside other conversions.
Smart Home Devices
Amazon Alexa, Google Home, and Apple Siri can convert temperatures: "Alexa, convert 25 Celsius to Fahrenheit." Response: 77 degrees Fahrenheit.
Programming and Code
In software development, temperature conversion is trivial. Most programming languages include:
Python: fahrenheit = (celsius * 9/5) + 32
Java Script: const fahrenheit = (celsius * 1.8) + 32;
These one-liners are used in countless weather apps, scientific software, and Io T devices.
Graphical Conversion Tools
Some tools display conversion graphs showing the relationship visually, which helps build intuition about how the scales relate.
Common Real-World Scenarios and Solutions
Let's walk through realistic situations and how conversion solves them.
Scenario 1: International Business Meeting
Situation: You're in a conference room in Toronto. A colleague from Germany says, "The facility operates at 22°C, but we need to increase to 25°C for the chemical process."
You need to understand: Is this a small change or significant?
Conversion:
- 22°C = 71.6°F
- 25°C = 77°F
- Change = 5.4°F
Understanding: That's a noticeable but not extreme increase in facility temperature. It's feasible and won't cause comfort issues for workers.
Scenario 2: Scientific Research Publication
Situation: You're writing a research paper. Your lab measured reactions at 37°C (standard body temperature for biological research). The journal requires both Celsius and Fahrenheit.
Solution: 37°C = 98.6°F. This benchmark is useful because readers immediately understand you were conducting human-relevant research.
Scenario 3: Freezer Temperature Check
Situation: You have a European refrigerator showing temperatures in Celsius. The freezer reads -18°C. Is this cold enough for food safety?
Conversion: -18°C = 0.4°F
Assessment: Yes, this is cold enough. USDA recommends 0°F or below for freezing; you're just slightly above. American freezers typically aim for -4°F to ensure safety margins. Your fridge is safe but could be colder for longer storage.
Scenario 4: Emergency Medical Response
Situation: An emergency room receives a patient from a country using Celsius. Vital signs show 39.5°C. The attending physician primarily works in Fahrenheit.
Rapid conversion: 39.5°C = 103.1°F
Assessment: High fever indicating serious infection. Immediate intervention protocol activated.
The few seconds saved by knowing conversion could matter in medical emergencies.
Educational Applications and Teaching Temperature Conversion
If you're teaching this topic, understanding common confusion points helps.
Why Students Struggle
Students often struggle because they're learning two new concepts simultaneously:
- The formula itself (which numbers multiply/add)
- The conceptual meaning (why these specific numbers?)
Teaching one without the other creates confusion. Explain the 9/5 ratio emerges from the 100-degree vs. 180-degree range, and the formula becomes logical rather than arbitrary.
Effective Teaching Sequence
- Start with reference points (0°C = 32°F, 100°C = 212°F)
- Calculate the ratio (180 ÷ 100 = 1.8)
- Derive the formula from reference points
- Practice conversion
- Build intuition through comparisons
Interactive Demonstrations
Using thermometers showing both scales, students can see the correspondence directly. Measuring temperatures of common objects (ice water, room temperature, hot water) creates concrete understanding.
Common Student Mistakes
Teachers see these regularly:
- Forgetting the +32
- Using 5/9 when converting to Fahrenheit (using the reverse formula)
- Not multiplying before adding
- Confusion about whether to add or subtract in reverse conversion
Emphasizing the logic (scale ratio first, offset second) prevents many errors.
The Future of Temperature Measurement
While Celsius and Fahrenheit seem permanent, measurement systems do evolve.
Why Fahrenheit Might Eventually Disappear
As globalization increases and the metric system dominates science, Fahrenheit's use continues shrinking. American adoption of metric measurements—even partial (soda sold in liters, scientists use Celsius)—suggests slow, generational change.
Future American generations might find Fahrenheit as quaint as Roman numerals for everyday use, even if scientific work remains in Celsius/Kelvin.
Digital Temperature Displays
Technology makes conversion trivial. Smart thermostats instantly display both scales. Weather apps show both. Weather forecasts could seamlessly present temperatures in whichever scale users prefer.
International Standards
As global temperature data becomes more critical for climate science, unified scales become more valuable. Celsius dominates this space. The IPCC (Intergovernmental Panel on Climate Change) uses Celsius exclusively.
Possible Solutions
Some propose:
- Temperature displays in all scales simultaneously
- Apps automatically converting based on user location
- Kelvin becoming more common for scientific applications
None of these eliminate Celsius or Fahrenheit—they just make conversion transparent.
Summary and Key Takeaways
Temperature conversion, while mathematically simple, reveals fascinating principles about measurement systems, historical development, and international standardization.
The formula °F = (°C × 1.8) + 32 is derived directly from the different ranges and reference points of the two scales. Understanding why this formula exists—rather than just memorizing it—makes conversion intuitive and reliable.
From travel planning to medical diagnostics to industrial processes, accurate temperature conversion touches countless real-world scenarios. The scenarios range from mundane (packing appropriate clothing) to critical (medical care and chemical manufacturing).
While technology makes instant conversion easy, understanding the underlying logic equips you with genuine comprehension rather than dependence on tools. When you grasp why Fahrenheit has 180 degrees and Celsius has 100, the 1.8 multiplication factor becomes obvious rather than arbitrary.
The persistence of two temperature scales in our modern world reflects historical accident and cultural entrenchment rather than logical necessity. But understanding both systems and their conversion makes you effective in a globally connected world where knowledge and communication cross borders constantly.
Whether you're converting a fever temperature for a doctor, setting an oven for an international recipe, or working in climate science, the conversion formula remains your reliable tool. Master it, understand it, and temperature translation becomes second nature.
FAQ
What is the exact formula for converting Celsius to Fahrenheit?
The formula is °F = (°C × 9/5) + 32, which can also be written as °F = (°C × 1.8) + 32. Both forms are mathematically identical. You multiply the Celsius temperature by 9/5 (or 1.8) to account for the different temperature scales, then add 32 to adjust for the different reference points between the two systems.
Why is 32 added in the Celsius to Fahrenheit conversion formula?
The number 32 is added because the freezing point of water is 0°C but 32°F. This offset accounts for the fact that the two temperature scales use different reference points. While Celsius starts its scale at water's freezing point, Fahrenheit starts at a different reference point entirely. The +32 adjustment ensures that temperatures align correctly between the two scales.
How do I convert negative Celsius temperatures to Fahrenheit?
The conversion formula works identically for negative temperatures. For example, to convert -10°C: multiply -10 by 1.8 to get -18, then add 32 to get 14°F. Negative Celsius temperatures are handled naturally by the mathematical operation and produce negative or lower Fahrenheit values as expected.
What temperature is the same in both Celsius and Fahrenheit?
The temperature -40 is the only point where Celsius and Fahrenheit scales show the same numerical value: -40°C = -40°F. This crossover point is mathematically determined and serves as a useful reference when approximating conversions or remembering that the two scales intersect at this single point.
Why do different countries use different temperature scales?
Fahrenheit and Celsius developed independently in different contexts and time periods. Fahrenheit was created first and became standard in Britain and America. Later, Celsius aligned with the decimal-based metric system and became the international standard for science and most countries. The United States retained Fahrenheit due to historical adoption and cultural entrenchment, while the rest of the world adopted the more logical metric system that includes Celsius.
How accurate is the quick estimation method of doubling Celsius and adding 30?
The formula °F ≈ (°C × 2) + 30 provides a rough approximation accurate to within 2-4 degrees for temperatures between 10°C and 30°C, which covers most everyday temperatures. While not precise enough for cooking or medical decisions, it's useful for quick mental estimates when you need a ballpark figure without access to a calculator or conversion tool.
What is the difference between a temperature point and a temperature interval in conversion?
A temperature point refers to an absolute measurement (like 20°C), which requires the full formula including the +32 offset when converting. A temperature interval or change (like "increased by 20°C") only requires multiplying by the scale ratio (9/5), as there's no reference point offset needed. This distinction matters in scientific contexts where temperature changes, rather than absolute values, are measured.
Can I use the same conversion formula for Kelvin temperatures?
No, Kelvin is an absolute temperature scale starting at zero (absolute zero), unlike Celsius and Fahrenheit which have arbitrary reference points. To convert Kelvin to Celsius, subtract 273.15: °C = K - 273.15. Then use the standard formula to convert to Fahrenheit. Scientists primarily use Kelvin because it's proportional to molecular kinetic energy and doesn't require negative numbers.
Why is the 9/5 ratio used in temperature conversion?
The 9/5 ratio (or 1.8 decimal equivalent) emerges directly from how the scales were constructed. Celsius divides the water freezing-to-boiling range into 100 equal degrees, while Fahrenheit uses 180 degrees for the same range. The ratio 180 ÷ 100 = 1.8, or expressed as a fraction: 9/5. This mathematical relationship is unavoidable given the scale definitions and isn't arbitrary.
How do I quickly convert Fahrenheit back to Celsius mentally?
For quick mental approximation, subtract 32 from the Fahrenheit temperature and divide by 2. This gives a rough estimate that's accurate within 1-2 degrees for everyday temperatures. For example, 68°F becomes (68 - 32) ÷ 2 = 18°C (actual: 20°C). While not perfectly precise, this method is much faster than the full calculation when you need a ballpark figure.
What professions most commonly need to convert between Celsius and Fahrenheit?
Medical professionals, chefs and food service workers, scientists and researchers, meteorologists, HVAC technicians, and engineers in international companies most frequently need these conversions. Medical professionals convert fever temperatures, chefs follow international recipes, scientists publish internationally, meteorologists communicate across regions, and technicians work with equipment from various manufacturers using different scales.
Key Takeaways
- The conversion formula °F = (°C × 1.8) + 32 is derived from the 100-degree Celsius range matching the 180-degree Fahrenheit range between water's freezing and boiling points
- The number 32 in the formula accounts for the reference point offset: 0°C equals 32°F for the freezing point of water
- Celsius dominates globally in science and most countries due to its alignment with the decimal metric system, while Fahrenheit persists primarily in the United States
- Quick approximation methods like doubling the Celsius temperature and adding 30 provide estimates within 2-4 degrees for everyday temperature ranges
- Temperature conversion is mission-critical in medical, culinary, scientific, and industrial applications where precision directly impacts outcomes
Related Articles
- iPhone 17 Pro Max Review: Design, Performance & Real-World Usability [2025]
- AI Data Center Boom vs Infrastructure Projects: The Resource War [2025]
- Angel Number 111 Meaning: Love, Career & Spirituality [2025]
- Tralalero Tralala Meme Explained: Parent's Complete Guide [2025]
- The Dark Side of Influencer Culture: Ethics, Accountability, and Online Safety [2025]
- 100+ Painting Ideas to Break Through Artist's Block [2025]
![Celsius to Fahrenheit Conversion: Complete Guide with Formulas [2025]](https://runable.blog/blog/celsius-to-fahrenheit-conversion-complete-guide-with-formula/image-1-1765664390797.jpg)



