AI Models Are Cracking High-Level Math Problems: Here's What's Happening [2025]

Introduction: When Machines Started Proving Theorems

Picture this: a software engineer pastes a mathematical problem into Chat GPT, hits enter, and walks away. Fifteen minutes later, he returns to find not just an answer, but a complete proof. He formalizes it with verification tools. It checks out.

This isn't science fiction anymore. This is happening right now, and it's reshaping how we think about artificial intelligence, mathematics, and the frontier of human knowledge.

For decades, we've told ourselves that mathematics was different. While AI could write decent code, generate images, or chat conversationally, real mathematics required human intuition, creativity, and years of specialized training. The gap between solving a simple algebra problem and tackling unsolved conjectures seemed unbridgeable.

Then something shifted.

Since Open AI released GPT 5.2, the mathematical capabilities of large language models have become impossible to ignore. We're not talking about incremental improvements or cherry-picked examples. Fifteen previously open mathematical problems moved from "unsolved" to "solved" status in just the past few weeks. Eleven of those solutions explicitly involved AI models working either independently or alongside human researchers.

This development raises questions that go beyond mathematics. If AI can now tackle problems that have stumped humanity's brightest minds for years or decades, what does that mean for the future of research? What does it mean for how we'll approach science, engineering, and discovery itself? And perhaps most importantly, what's actually happening under the hood when these models crack problems?

The answer involves unexpected breakthroughs in reasoning, a quiet revolution in mathematical formalization, and a growing acceptance among elite mathematicians that these tools aren't just calculators—they're becoming genuine research partners.

Let's dig into what's really going on.

TL; DR

• AI models are solving the Erdős problems: Since Christmas 2025, 15 previously unsolved mathematical conjectures have been solved, with 11 involving AI models directly (The Neuron Daily).
• GPT 5.2's breakthrough reasoning: The latest GPT iteration shows dramatically improved mathematical reasoning, combining axioms and historical research to find novel proofs (eWeek).
• The role of formalization tools: Proof assistants like Lean and Aristotle are making it easier to verify and extend AI-generated mathematics (Lean).
• Elite mathematicians are taking notice: Leaders like Terence Tao are documenting AI's autonomous progress on open problems (Wikipedia).
• This changes research workflows: AI tools are becoming essential for literature review, problem exploration, and formalization across mathematics (MIT News).

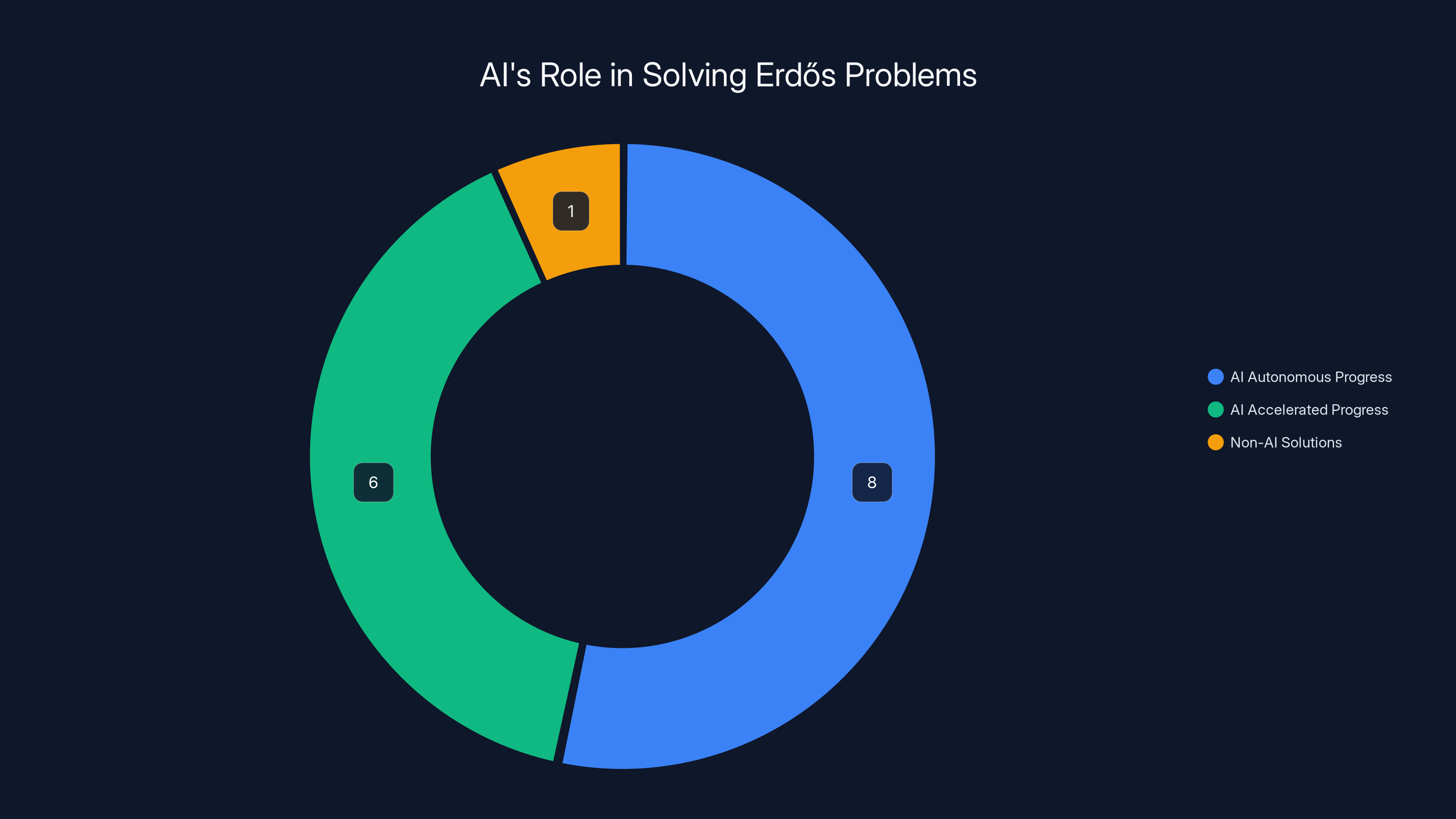
AI models contributed to solving 14 out of 15 problems on the Erdős list, with 8 solved autonomously and 6 with AI-accelerated progress. Estimated data.

The Breakthrough That Changed Everything: Neel Somani's Discovery

The story starts with Neel Somani, a software engineer with a background in quantitative research and startup founding. He wasn't trying to make headlines. He was simply curious: at what point does an AI model actually become useful for solving genuine mathematical problems?

So he took some unsolved problems from the Erdős collection and started testing. The Erdős problems are no joke. They come from Paul Erdős, a legendary Hungarian mathematician who spent his career proposing conjectures across number theory, combinatorics, graph theory, and other fields. Over a thousand problems remain, varying wildly in difficulty. Some might be solvable with clever insights. Others have resisted attack for decades.

What Somani discovered was stunning: when he fed certain problems to Chat GPT with its new extended chain-of-thought capabilities, the model didn't just produce an answer. It produced a complete, verifiable proof.

The approach itself was elegant. Chat GPT would invoke mathematical axioms like Legendre's formula and Bertrand's postulate, working through logical steps with the kind of rigor you'd expect from a published paper. At one point, it even located a 2013 post from Harvard mathematician Noam Elkies that contained a related solution. The model synthesized this with its own reasoning and produced something even more complete than Elkies' original work—a solution that tackled a harder variant of the problem.

What makes this remarkable isn't just that it worked. It's that the model's proof diverged meaningfully from human solutions while remaining correct. This suggests something deeper than retrieval or memorization. The model appears to be engaging in genuine problem-solving.

The Erdős Problems: A Perfect Testing Ground for AI

To understand why this matters, you need to understand what the Erdős problems represent.

Paul Erdős was prolific in a way that's almost hard to comprehend. During his lifetime, he published over 1,500 papers. He collaborated with hundreds of mathematicians. And he had a peculiar habit: he would pose problems. Thousands of them. Some were serious research directions. Others were playful explorations. All of them were mathematically interesting.

Today, the Erdős problem list maintained online contains over 1,000 conjectures. What makes this collection perfect for AI benchmarking is the diversity. These problems span different mathematical domains, require different toolsets, and vary dramatically in difficulty.

Some problems are elementary enough that a talented undergraduate might crack them. Others have resisted the world's best mathematicians for sixty years. They're ranked by difficulty and prize money. A

Why are these valuable for testing AI? Because they're not academic exercises. They're real, open questions. They appear in legitimate mathematical literature. A solution counts as a genuine contribution to mathematics, not a parlor trick.

For AI researchers and mathematicians alike, the Erdős problems function like a leaderboard. If you claim an AI can do serious mathematics, prove it by solving an Erdős problem. And starting this past December, the results became impossible to ignore.

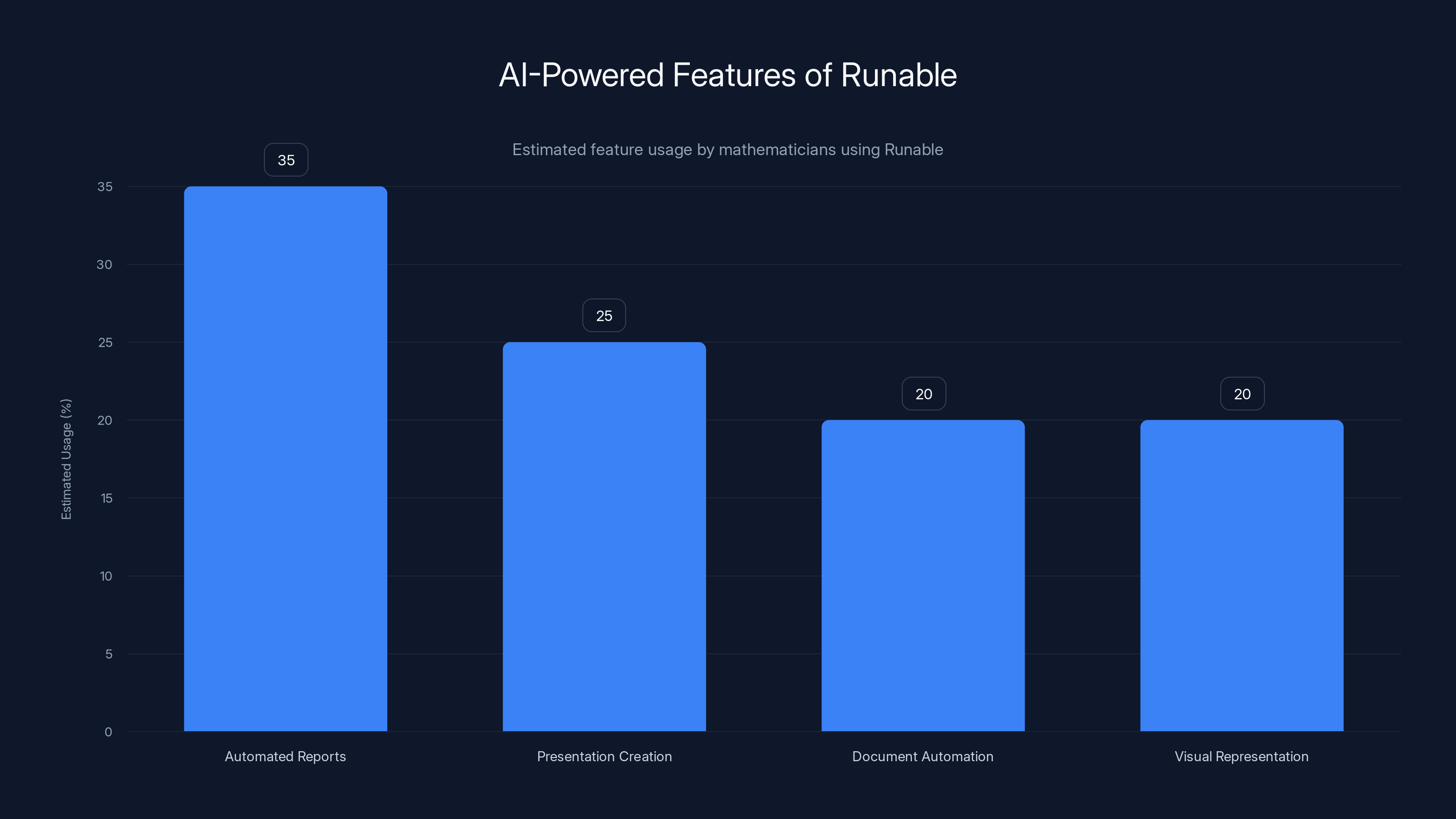
Runable's AI-powered features are estimated to be most utilized for automated report generation, enhancing efficiency in mathematical research workflows. Estimated data.

The Data: 15 Problems Solved in Weeks

Let's look at the hard numbers, because they tell the story most clearly.

Since Christmas 2025, exactly 15 problems on the Erdős list moved from "open" to "solved." Of those 15, 11 involved AI models in their solutions. This is in a timeframe of roughly four weeks.

To put that in perspective, consider how problems are normally solved. The Erdős list has been maintained for decades. New solutions appear sporadically. Having 15 problems solved in a month would be extraordinary under any circumstances. Having 73% of those involve AI models is genuinely unprecedented.

The first batch came from Google Deep Mind's Alpha Evolve in November, which used Gemini capabilities to tackle problems autonomously. But the more recent surge came from GPT 5.2, which Open AI released in late 2024.

Terence Tao, perhaps the most prominent research mathematician currently active, documented these successes on his Git Hub page. Tao identified eight problems where AI models made meaningful autonomous progress without direct human intervention. Additionally, he found six cases where AI accelerated problem-solving by finding and building on previous research.

This distinction matters. Autonomous progress means the AI solved it independently. Accelerated progress means the AI helped humans solve it faster. Both represent genuine advancement.

Tao's analysis suggests something important: the capacity varies by problem. Some problems are straightforward enough that an AI can work through them independently. Others require human insight, but AI tools speed up the research process dramatically.

The type of problems being solved is also worth noting. They're not trivial. These are genuine mathematical problems that would merit publication in journals if solved by humans. The fact that AI solved them doesn't diminish the difficulty—it just shifts who the solver is.

GPT 5.2's Mathematical Breakthrough: What Changed

So what exactly makes GPT 5.2 different from earlier versions?

The most obvious feature is extended chain-of-thought reasoning. When you submit a problem to GPT 5.2, you can ask it to "think" for extended periods. Instead of rushing to an answer in seconds, the model takes 10, 15, or sometimes 20+ minutes to work through the problem step-by-step.

This might sound simple, but it's fundamentally different from how earlier models worked. Previous versions would generate text sequentially, optimizing for speed. GPT 5.2 can now spend computational resources on deep exploration of a problem space.

During this extended thinking period, something remarkable happens. The model doesn't just concatenate random theorems. It actually constructs logical chains. It invokes specific mathematical axioms at relevant moments. It explores dead ends and backtracks. It references historical solutions and builds on them.

Why does this work? The answer involves how large language models actually process information. These models are fundamentally pattern-matching systems trained on vast datasets of text. When trained on mathematical papers, textbooks, and problem solutions, they learn patterns about how mathematics works. They learn that certain axioms precede certain theorems. They learn the structure of proofs.

When given extended time to think, the model can essentially explore its learned pattern space more thoroughly. It can consider more possible next steps. It can evaluate more branches of reasoning. It's not thinking like a human, but it's doing something functionally similar to deeper exploration.

Another key improvement is improved axiomatic reasoning. Earlier models would sometimes invoke mathematical concepts incorrectly or anachronistically. GPT 5.2 demonstrates much stronger understanding of which axioms are relevant for which problems. It knows that Legendre's formula applies to certain number-theoretic contexts. It recognizes when Bertrand's postulate might help.

This suggests the model has developed something like mathematical intuition—which is genuinely shocking for a statistical pattern-matching system.

The Role of Formalization: Making Math Verifiable

Here's something that might surprise you: solving a problem and formally proving it are different things.

You can have a correct mathematical proof that's written informally, using natural language, with some steps implied or hand-waved. Mathematicians do this all the time. It's acceptable because other expert mathematicians can fill in the gaps.

But there's a problem with this approach when AI is involved. How do you verify an AI's proof? You can't just trust it. You need to check it rigorously. And informal proofs are hard to verify programmatically.

This is where formalization becomes crucial.

Formalization means taking a proof and rewriting it in a formal language that a computer can verify automatically. Instead of "it's obvious that x follows from y," you have explicit logical steps. Instead of implicit axioms, every assumption is stated. The result is something a machine can check for logical consistency.

For years, formalization was a laborious, human-intensive process. You'd write a proof. Then you'd spend weeks or months translating it into formal language. It was so tedious that most mathematicians avoided it unless absolutely necessary.

But recent advances have changed this dramatically.

Lean, an open-source proof assistant developed at Microsoft Research, has become the industry standard. Lean lets you write mathematical proofs in a formal language that's checked automatically. If your proof has a gap, Lean tells you. If your logic is wrong, Lean catches it.

The breakthrough is this: AI tools can now help automate formalization itself.

Tudor Achim, founder of Harmonic, built Aristotle, an AI tool specifically designed to assist with formalization. Aristotle doesn't solve mathematical problems. Instead, it helps convert informal proofs into formal language. It suggests how to structure arguments. It identifies where additional lemmas are needed. It dramatically reduces the human effort required.

What this means practically: when Somani solved an Erdős problem using Chat GPT, he could then use Aristotle to formalize the solution quickly. The proof moved from a chatbot output to a verified, machine-checked piece of mathematics in hours rather than weeks.

This creates a powerful feedback loop. AI generates solutions. Formalization tools verify them. Verified solutions advance mathematics. The entire process accelerates.

Achim's perspective is telling. When asked about the significance of recent Erdős solutions, he emphasized that what really matters isn't the problems themselves. It's that elite mathematicians are now using these tools regularly. "These people have reputations to protect," he explained. "When they're saying they use Aristotle or they use Chat GPT, that's real evidence."

When a prestigious mathematician stakes their reputation on trusting an AI tool, you know something has fundamentally changed.

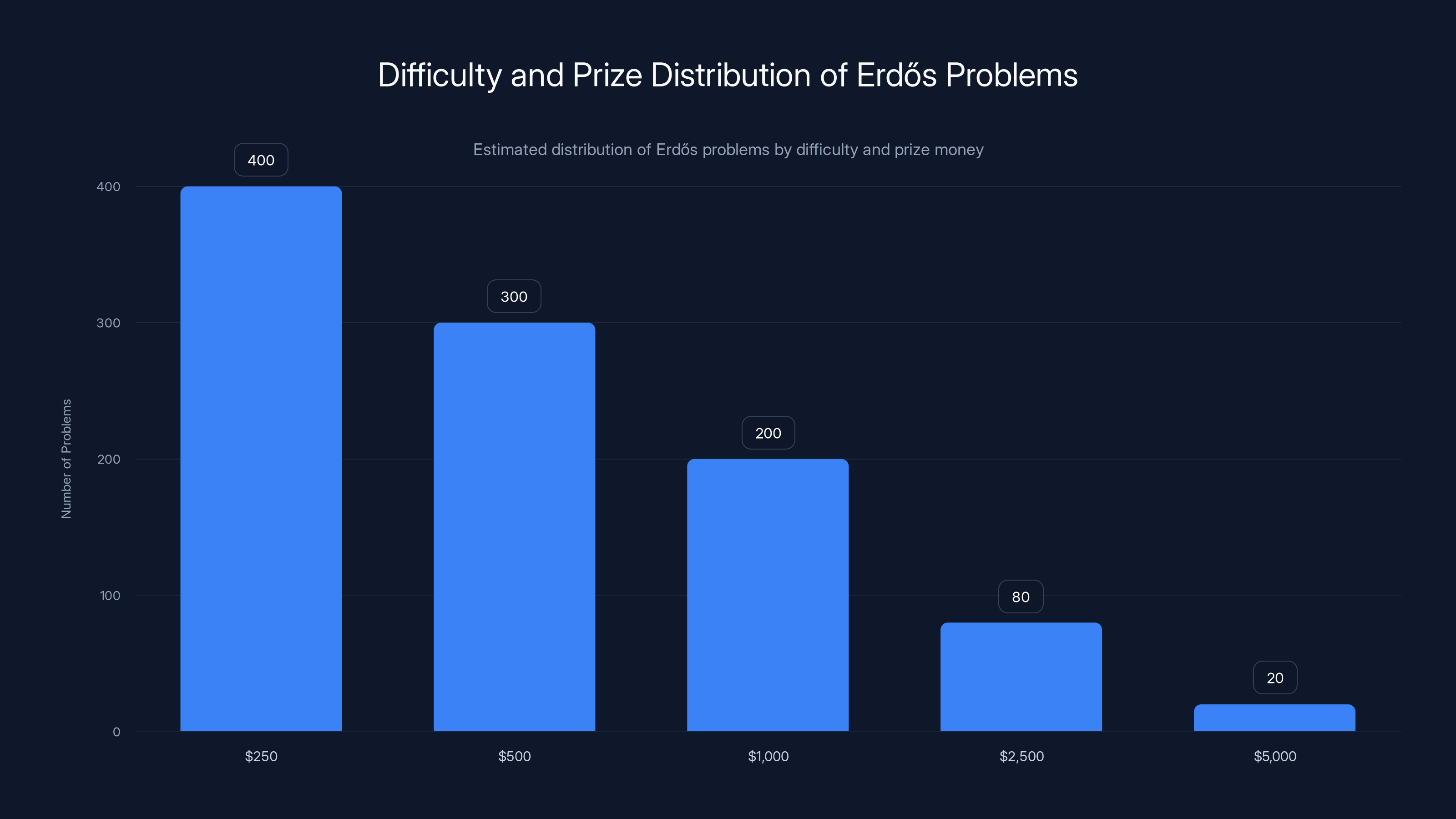
Estimated data shows a higher number of Erdős problems with lower prize money, indicating more accessible challenges for AI and mathematicians.

Why These Problems Are Different: Open vs. Closed Mathematics

To understand the significance of solving Erdős problems, you need to understand the difference between closed and open mathematics.

Closed mathematics problems have well-defined answers that can be verified. Solve for x. Compute the integral. Find the prime factors. Either you're right or you're wrong.

AI has been good at closed problems for a while. Feed it a calculus problem, and it can usually work through it. Not perfectly, but reasonably well.

Open mathematics problems are different. They're questions about whether something is true, and nobody knows the answer. Maybe it's true, maybe it's false, maybe it's undecidable. Solving an open problem means finding a proof (or counterexample) that convinces the mathematical community.

This is much harder. You can't just compute an answer. You have to construct novel reasoning. You have to make conceptual leaps. You have to be creative.

For the longest time, this seemed out of reach for AI. Creativity felt like something inherently human. Open-ended mathematical reasoning felt like the domain of genius, not algorithms.

Except now it's not.

The Erdős problems that have been solved recently are open problems. Real ones. They required actual reasoning, not just calculation. Some required exploring multiple approaches. Some required synthesizing ideas from different mathematical domains. Some required seeing connections that aren't obvious.

The fact that AI can do this, even if imperfectly and sometimes with human guidance, fundamentally changes how we think about both AI and mathematics.

The Mechanism: How AI Solves Problems It's Never Seen

Let's talk about what's actually happening when GPT 5.2 solves a problem.

When you submit a novel mathematical problem to the model, it has never seen that exact problem before. It doesn't look up the answer. It has no memorized solution. Instead, the model is doing something much more interesting: it's applying learned patterns about how to construct mathematical arguments.

Think of it this way. The model was trained on decades of mathematical papers, textbooks, and proofs. During training, it learned statistical patterns about:

• How mathematicians introduce definitions
• Which axioms typically precede which theorems
• How logical steps connect
• What kinds of techniques work for which problem classes
• How to transition from problem setup to solution

When you give the model a new problem, it essentially draws on this learned pattern library to construct a response. It's not conscious reasoning in the human sense. But it's also not just random text generation.

The extended thinking capability amplifies this. By spending more computation time on the problem, the model can explore more branches of its pattern space. It can consider more possible approaches. It can evaluate which paths lead toward coherent proofs versus dead ends.

There's something almost like search happening here, except it's happening in the space of mathematical patterns rather than the space of premade solutions.

Another factor is cross-domain transfer. Mathematical knowledge is deeply connected. A technique from number theory might apply to a combinatorics problem. A method from algebra might help with a geometry problem. The model's training on broad mathematical literature means it has learned these connections. When solving a novel problem, it can draw on techniques from seemingly unrelated domains.

This is actually hard for humans to do consistently. We tend to specialize. A number theorist might not immediately see how a combinatorial technique applies to their problem. But the model, having seen mathematical papers from many domains, makes these connections naturally.

Does this mean the model truly understands mathematics? That's philosophically complex. It's not understanding in the conscious sense. But it's something more than mere pattern matching too. It's learned the deep structure of how mathematical reasoning works.

Real-World Impact: How Researchers Are Actually Using These Tools

The theoretical breakthrough is fascinating. But let's talk about actual usage.

Mathematicians and computer scientists are integrating these tools into their workflows in concrete ways. It's not just hobbyists playing with Chat GPT. It's serious researchers using AI as part of their research process.

Literature Review Acceleration: Previously, diving into an obscure mathematical topic meant spending days or weeks reading papers. Now, researchers use AI tools to summarize the state of knowledge quickly. What used to take a week can happen in an afternoon. A researcher can ask, "What's been proven about Goldbach's conjecture in relation to prime gaps?" and get a synthesized summary with citations.

Conjecture Exploration: Before diving into a proof attempt, mathematicians now use AI to explore a conjecture's landscape. Does it have been studied before? Are there related problems? What techniques have been tried? This exploration phase, which used to require significant background research, now happens instantly.

Proof Sketching: Researchers sketch out the rough shape of a proof using AI. "If I could prove this lemma, would that imply the main result?" The model helps work through the logical structure. Once the skeleton is clear, the human mathematician verifies each step rigorously.

Formalization Assistance: As mentioned, tools like Aristotle help convert informal proofs to formal ones. A researcher can focus on the mathematical content while the tool handles the technical formalization work.

Debugging Proofs: When a proof isn't working, researchers ask the model where the logic breaks down. The model often identifies subtle logical gaps that humans might miss, especially in complex, multi-step proofs.

Tudor Achim's observation is key here: mathematicians with reputations are using these tools. Not anonymously, not experimentally, but openly. When a mathematician publishes a paper crediting AI, that's a strong signal that the tool is genuinely useful, not just hype.

What's particularly interesting is that the leading users aren't trying to minimize human involvement. They're not trying to remove themselves from the process. They're using AI as a thinking partner. The mathematician provides the insight and direction. The AI provides raw reasoning power and breadth of knowledge.

It's a partnership model, and it's clearly working.

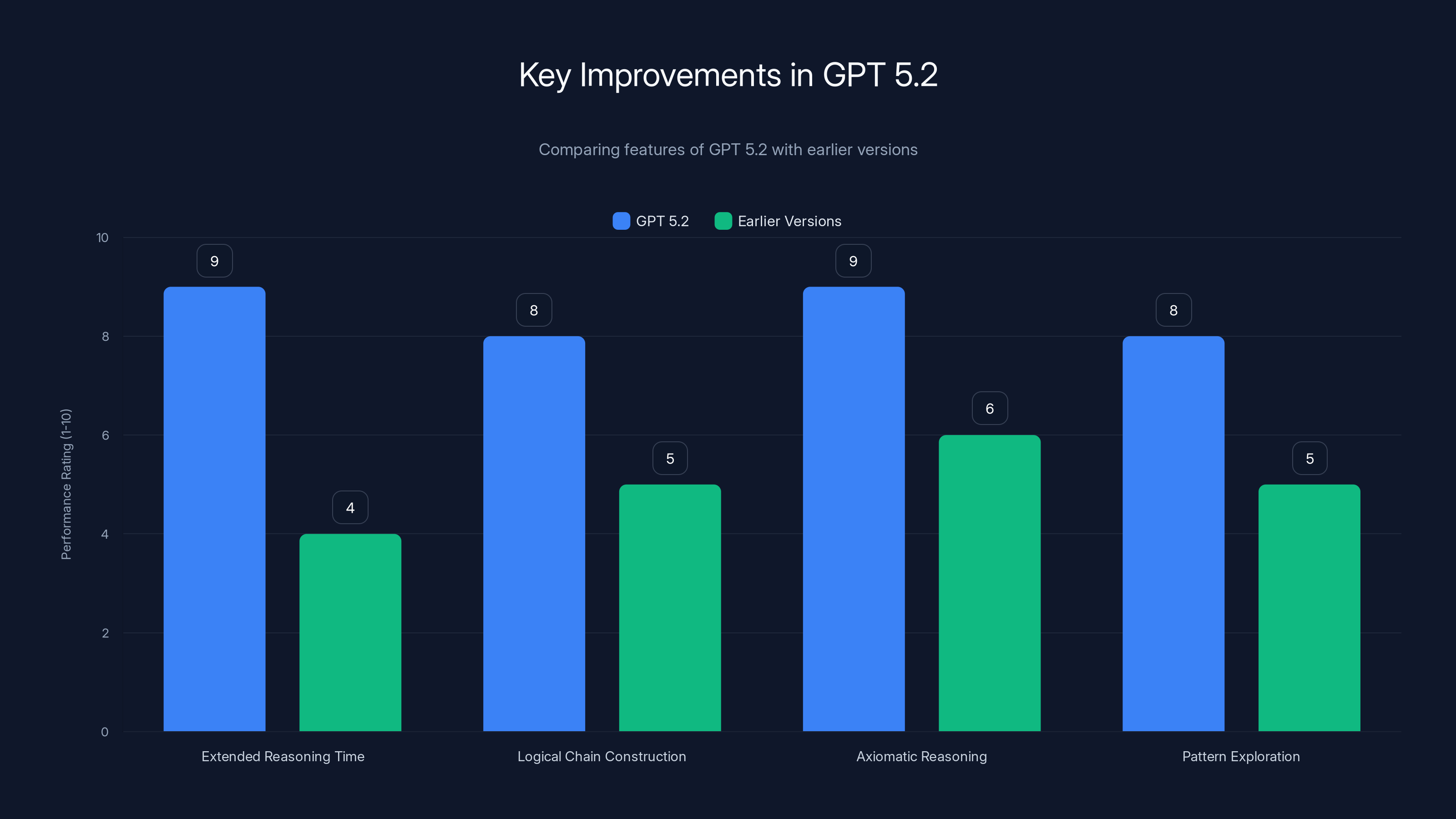
GPT 5.2 shows significant improvements in extended reasoning time and logical chain construction compared to earlier versions, enhancing its mathematical problem-solving capabilities. Estimated data.

The Limitations: What AI Still Can't Do

Before we get too excited, let's be clear about what's not happening.

AI is not replacing mathematicians. The solved Erdős problems are interesting, but they're still a tiny fraction of open problems. Many problems remain completely beyond AI's current reach. Some might always be.

There are fundamental limitations:

Conceptual Breakthroughs: Some mathematical progress requires genuinely new ideas. A framework that nobody has thought of before. A connection between disparate areas that suddenly unlocks problems. These kinds of breakthroughs seem to require human insight. AI is still, fundamentally, pattern-matching on existing patterns. Creating genuinely new patterns might require something different.

Verification Challenges: Just because an AI produces a proof doesn't mean it's correct. Formalization helps, but formalization itself can have errors. Someone still needs to understand the proof deeply enough to trust it. This requires human expertise.

Deep Intuition: The best mathematicians don't just know techniques. They have intuitions about what should be true. Why certain approaches might work. Where to focus effort. This kind of intuitive guidance still seems to be a human strength.

Originality Uncertainty: When AI solves a problem, it's sometimes hard to know if the solution is truly novel or if it's essentially reproducing a known approach it absorbed during training. The solution to the Erdős problem that Chat GPT found differed from published solutions, but did it represent a genuinely original insight? That's subjective.

Scalability of Difficulty: Harder problems require longer chain-of-thought. There are computational limits. You can't just ask the model to think for an hour. At some point, extended thinking becomes impractical.

Terence Tao himself emphasizes this nuance. AI is working well on easier problems that have straightforward solutions. The problems where AI has made "autonomous progress" tend to be more amenable to systematic approach. Harder problems still require human direction.

Tao's suggestion is that AI is ideally suited for the "long tail" of obscure problems. The ones that aren't famous, don't have big prizes, but still matter. Historically, these problems get solved slowly because they're not high-priority research targets. AI can work through them systematically.

But this is different from saying AI is pushing the absolute frontier of mathematics. That still requires human genius.

The Formalization Revolution: From Tedious to Automated

Let's zoom in on formalization because it's genuinely important and often underappreciated.

Historically, formal verification was the domain of specialists. If you needed a mathematical proof verified by a computer, you'd hire someone with expertise in proof assistants. It was expensive, slow, and usually only done for critical systems like aircraft control software or cryptographic protocols.

Mathematicians largely ignored formalization. Their proofs were published in journals, reviewed by peers, and accepted based on community consensus. Formalization seemed unnecessary—even obstructive.

But there's been a quiet shift. Several factors have aligned:

Lean Development: Lean has matured significantly. It's easier to use. The documentation is better. The community has grown. Major mathematical results have been formalized—everything from the four-color theorem to fundamental topology. This creates momentum.

Mathlib Creation: Mathlib is a library of formalized mathematics in Lean. Instead of starting from scratch, mathematicians can now build on thousands of already-formalized results. This dramatically reduces the work required to formalize new proofs.

AI-Assisted Formalization: Tools like Aristotle make the process semi-automatic. You don't need to hand-translate every step. The AI handles the tedious parts.

Computational Verification: When proofs are formalized, they can be checked by computer in seconds. No possibility of a subtle logical error slipping through. This is actually valuable even beyond verification—it gives confidence in correctness.

The result is a positive feedback loop. More formalized mathematics makes future formalization easier. AI tools make formalization faster. More results get formalized. The ecosystem strengthens.

Why does this matter beyond mathematical purity? Because formal verification creates permanent records. A proof published in a journal might be out of print in ten years. A formally verified proof persists, checkable forever.

For AI-generated mathematics especially, this is crucial. If all solutions are formally verified, we have clear evidence that they're correct. This builds trust.

We're at an interesting inflection point. Formalization might shift from rare specialty to standard practice. And that changes what's possible.

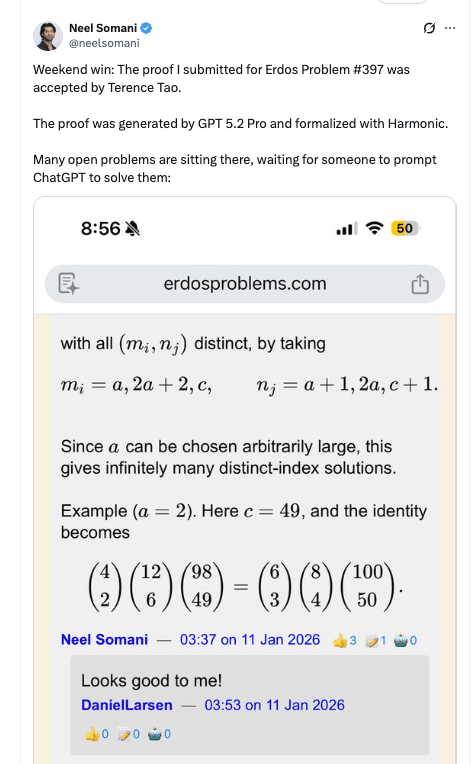
Terence Tao's Analysis: What One of the World's Greatest Mathematicians Thinks

To understand the significance of recent breakthroughs, pay attention to Terence Tao.

Tao is not a casual observer. He's a Fields Medalist, UCLA professor, and arguably the most influential pure mathematician alive today. His opinion carries weight. When Tao says something about AI and mathematics, mathematicians listen.

On his Git Hub, Tao documented specific cases where AI made meaningful progress on Erdős problems. He identified eight cases of autonomous progress and six cases of accelerated progress. But more importantly, he offered nuanced commentary.

Tao's key insight: AI systems are "scalable." Humans are limited. We can only work on so many problems, spend so much time thinking. But AI can be deployed systematically across thousands of problems. It can explore the long tail of neglected problems. It can try approaches that humans might not consider because they seem tedious.

This scalability advantage is particularly powerful for problem classes that have straightforward solutions. For problems where you just need to try enough approaches, AI excels. It can try approaches in parallel. It can explore combinations that would take humans years.

For problems requiring genuine conceptual breakthroughs, AI is still limited. But for routine problem-solving, formalization, and exploration, AI is becoming indispensable.

Tao's framing is important because it's not hype. He's not saying AI will solve all mathematics or replace mathematicians. He's identifying a specific niche where AI adds genuine value and being precise about it.

This kind of measured endorsement from elite mathematicians is significant. It means these tools are past the "interesting experiment" phase. They're becoming actual research infrastructure.

Since December 2024, AI models have solved 15 mathematical conjectures, with a significant portion solved through human-AI collaboration. Estimated data.

The Timeline: How We Got Here

Understanding how we got to this point requires looking at the convergence of several technologies.

2013: Lean is developed at Microsoft Research. At the time, it's interesting but niche—a tool for specialists interested in formal verification.

2017-2020: Transformer architecture enables large language models. Open AI, Deep Mind, and others begin developing large models. Initial math capabilities are modest but better than before.

2021-2023: LLMs improve rapidly. Mathematical reasoning still lags behind natural language, but the gap narrows. Tools start being built around LLMs for specific domains.

2023-2024: Chain-of-thought prompting is discovered. This technique of asking models to show reasoning step-by-step dramatically improves performance on complex problems.

November 2024: Google Deep Mind releases Alpha Evolve, a Gemini-powered system that autonomously solves problems. First batch of Erdős solutions.

Late 2024: Open AI releases GPT 5.2 with extended chain-of-thought capabilities. Mathematics performance jumps significantly.

December 2024-January 2025: The acceleration begins. Researchers test GPT 5.2 on Erdős problems. Results exceed expectations. Within weeks, 15 problems are solved.

Ongoing: Formalization tools mature. Mathlib expands. More mathematicians experiment with AI. Tools specifically designed for mathematical reasoning (like Harmonic's Aristotle) launch and improve.

This timeline shows something important: we didn't suddenly achieve a breakthrough. It was a series of incremental improvements across multiple dimensions that converged. Better base models, better prompting techniques, better formalization tools, better training data.

When all these pieces aligned, the capability jump became dramatic. But there's no single breakthrough. Just convergence.

Comparing AI to Human Mathematical Problem-Solving

How does AI's approach to mathematics compare to how humans do it?

Humans typically:

1. Build intuition by working on many related problems over months or years
2. Develop pattern recognition for which techniques apply where
3. Make conceptual leaps by suddenly seeing connections
4. Work incrementally, often proving smaller lemmas first
5. Get stuck and try different approaches when something isn't working
6. Collaborate by explaining ideas to others and hearing feedback

AI models:

1. Train on patterns from existing mathematics without conscious understanding
2. Process at scale across vast amounts of information simultaneously
3. Explore systematically by examining many possible directions
4. Construct proofs by chaining logical steps based on learned patterns
5. Lack the breakthrough insight that sometimes solves hard problems
6. Don't truly collaborate but rather respond to prompts

The differences are significant. Humans are good at the hard part: seeing why something is true. AI is good at the systematic part: verifying that a particular approach works.

When combined, they're stronger than either alone. The human provides direction and insight. The AI provides systematic exploration and formalization. Together, they solve problems neither could alone.

This might be the most important insight: the future of mathematics isn't AI replacing humans or humans replacing AI. It's human-AI teams that leverage both strengths.

The Broader Implications: What This Means for Research

The Erdős problems represent a narrow domain, but the implications are broad.

If AI can crack open mathematical problems, what about other fields?

Physics: Theoretical physics relies on mathematical intuition and exploration. Could AI help discover new physical laws? Some researchers think so.

Computer Science: Algorithm design often involves mathematical reasoning. Could AI help find better algorithms? There's early evidence it can.

Engineering: Many engineering problems reduce to mathematical optimization. Could AI speed up designs? Absolutely.

Biology: Protein folding, genetic analysis, drug discovery—all involve computational mathematics. AI is already making inroads here.

Mathematics is arguably the hardest domain for AI to tackle. If AI can make progress here, progress elsewhere might come faster.

This suggests a future where AI is deeply embedded in research across many fields. Not replacing researchers, but augmenting them. A future where breakthroughs come faster because AI handles the computational heavy lifting while humans focus on insight.

This could accelerate scientific progress dramatically. Or it could change what "breakthrough" means when machines are contributing equally.

We're in genuinely unprecedented territory.

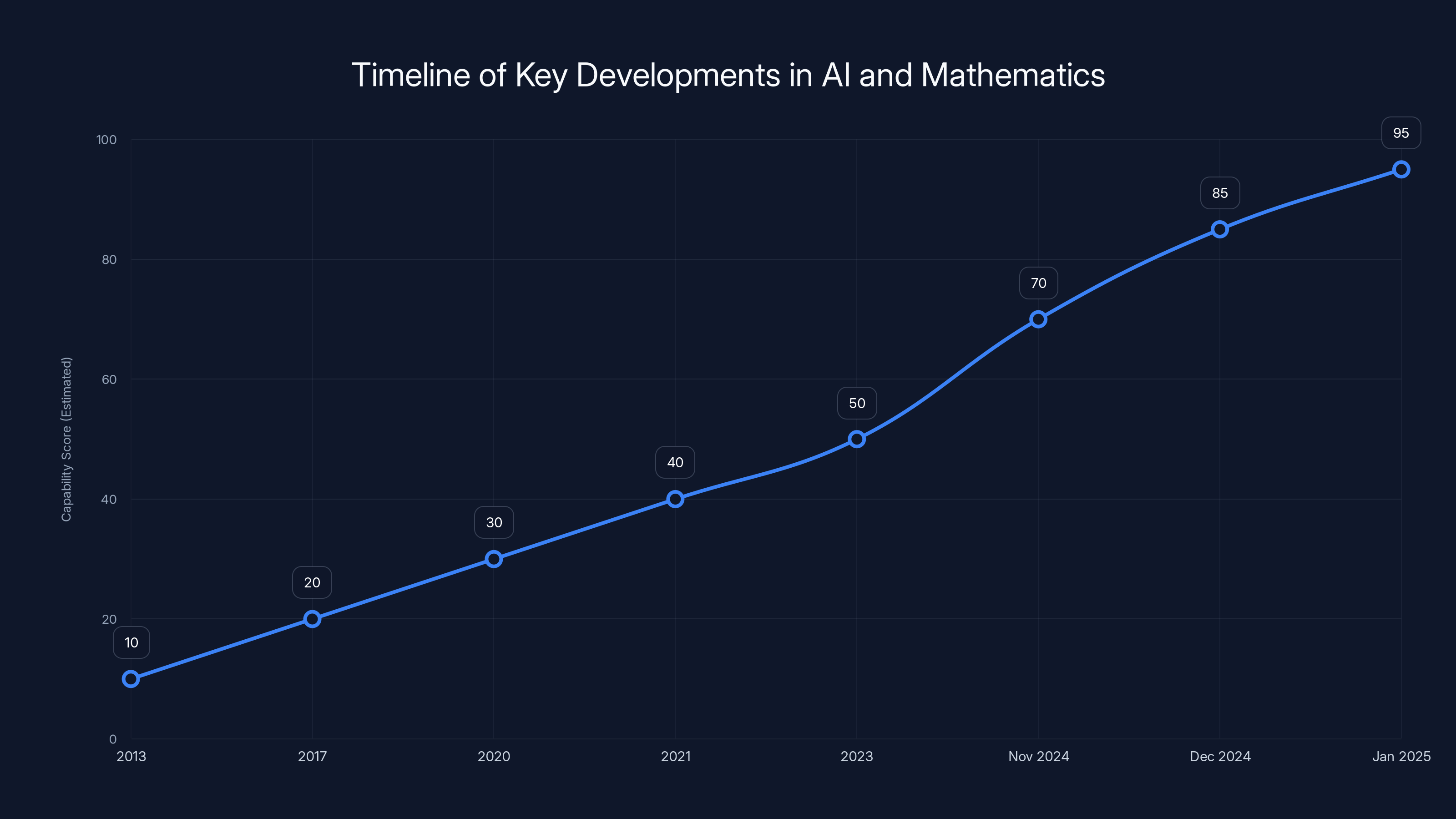
The timeline illustrates a steady improvement in AI's mathematical reasoning capabilities, with significant leaps in late 2024 due to advancements in chain-of-thought prompting and model releases. Estimated data.

Challenges and Concerns: The Counterarguments

Not everyone is optimistic about AI in mathematics.

Some concerns:

Reproducibility: When AI generates a solution, can it explain why it works? If not, have we really learned anything? There's a philosophical question here about what mathematical understanding means.

Trust and Verification: How much effort goes into verifying AI solutions? If verification is as hard as solving from scratch, there's no net benefit.

Intellectual Property: If an AI trained on published math discovers something new, who deserves credit? This gets legally complex.

Job Implications: If AI can solve problems, what happens to mathematicians whose value came from solving hard problems?

Dependence: Could reliance on AI tools create skills atrophy? Could mathematicians become dependent on AI for reasoning they should do themselves?

These concerns are legitimate. They're not reasons to reject AI tools, but reasons to be thoughtful about how they're integrated.

Some solutions:

• Formal verification standards: Require AI-generated proofs to be formally verified
• Contribution clarity: Be explicit about AI's role in any publication
• Skill maintenance: Ensure mathematicians understand proofs AI produces
• Transparency: Use AI as a tool while maintaining human responsibility for results

The goal isn't to eliminate AI use but to use it wisely.

The Future of Mathematical Research: What's Next

If this trajectory continues—and there's no reason to think it won't—what does mathematics look like in five years?

Widespread AI Tool Use: Most mathematicians will have AI as a standard research tool. Using Chat GPT or its equivalent for exploration will be normal, like using computational tools is now.

Faster Problem Resolution: Currently unsolved problems get solved faster. Not all of them, but many in the long tail. The average time from proposal to solution might compress significantly.

Formalization as Default: More proofs get formally verified. Standards evolve. Maybe formal verification becomes required for major results.

New Problem Classes: As old problems get solved, new ones emerge. Mathematics doesn't run out—it evolves. New frontiers open.

Integration with Computation: The line between "pure math" and "computational math" blurs further. Most proofs will have computational components verified by machines.

Human Insight Remains Premium: The hardest, most conceptually demanding problems still require human creativity. But they require it at higher levels—the AI handles routine reasoning.

Skill Evolution: Mathematicians learn to work with AI. The skill set shifts from "solve this problem" to "direct this problem-solving tool effectively." New abilities become valuable.

One particularly interesting possibility: AI might make certain types of mathematics more accessible. If formalization can be automated, maybe more people can do research-level mathematics. The barrier to entry could lower.

Or it could concentrate research further among those who have the best AI tools and strongest ability to direct them.

The outcome depends heavily on choices we make now about how tools are developed, distributed, and regulated.

Runable's Role in AI-Powered Mathematical Work

For researchers looking to integrate AI into their workflows more comprehensively, platforms like Runable offer solutions beyond traditional mathematical tools.

Runable provides AI-powered automation for creating documents, presentations, reports, and structured content at $9/month. For mathematicians working on publishing or presenting research, this means:

• Automated report generation from mathematical analysis
• Presentation creation from research data
• Document automation for papers and proposals
• Visual representation of mathematical concepts

While Runable doesn't specifically solve math problems, it accelerates the research-to-publication pipeline. Mathematicians spend less time on formatting and presentation, more time on mathematics itself.

Conclusion: A New Era of Mathematical Discovery

We're witnessing something genuinely significant. For the first time, artificial intelligence is contributing meaningfully to the solution of open mathematical problems.

This isn't hype or marketing. It's concrete: 15 problems solved in weeks, with elite mathematicians acknowledging the contribution.

The mechanism is interesting: large language models have learned the deep structure of mathematical reasoning well enough to make novel contributions. Chain-of-thought thinking allows them to explore problems methodically. Formalization tools verify results automatically. The entire research workflow is being augmented.

But this is still the early stage. AI isn't replacing mathematicians or solving fundamental open problems autonomously. What's happening is more nuanced. AI is becoming a research partner—a tool that excels at systematic exploration, formalization, and literature synthesis.

The mathematicians driving this forward aren't trying to reduce human involvement. They're enhancing it. They're asking: what can we accomplish if we combine human insight with machine reasoning power?

The answer, so far, is: more than either could alone.

This has implications beyond mathematics. If machines can tackle open-ended mathematical problems, they can likely tackle open-ended problems in physics, biology, engineering, and other fields. The barrier that seemed absolute—that only humans could do creative, original research—has been crossed.

It's not a complete crossing. But it's a beginning.

The next few years will be crucial. How do we integrate these tools? What standards do we establish for AI-assisted research? How do we ensure that accessibility remains broad? These questions matter as much as the technical capabilities themselves.

One thing is certain: mathematics will never be quite the same. The days of assuming that advanced research is purely a human domain are over.

The future of mathematical discovery is collaborative. Human insight directing. Machine reasoning executing. Together, solving problems faster than ever before.

It's exhilarating, slightly scary, and undeniably real.

FAQ

What exactly did AI models solve recently?

AI models solved 15 previously open mathematical conjectures from the Erdős problem list since late December 2024. Eleven of these solutions involved AI models like Open AI's GPT 5.2 or Google Deep Mind's Alpha Evolve, either working independently or assisting human researchers. These are genuinely difficult open problems in mathematics, not trivial exercises.

How does GPT 5.2 solve problems it's never seen before?

GPT 5.2 uses extended chain-of-thought reasoning to explore problems systematically. Rather than jumping to conclusions, it takes time to work through logical steps, invokes relevant mathematical axioms, considers multiple approaches, and synthesizes ideas. The model learned patterns about how mathematical reasoning works from its training data on mathematical papers and textbooks. When solving a novel problem, it draws on these learned patterns to construct novel proofs. This isn't conscious understanding, but it functions similarly to deep mathematical exploration.

What role do formalization tools like Lean play in this process?

Lean and related proof assistants allow mathematicians to convert informal proofs into formal language that computers can verify automatically. Tools like Harmonic's Aristotle automate much of this formalization work, making it practical to formally verify AI-generated proofs. This verification is crucial because it provides absolute confidence that proofs are logically correct. Without formalization, trusting AI-generated mathematics would be much harder.

Are AI models actually creating new mathematical knowledge or just retrieving existing knowledge?

AI models are doing something genuinely novel. While they're trained on existing mathematics, they're combining knowledge in new ways to solve problems they've never encountered. The proofs they generate often differ from published solutions and sometimes are more elegant or complete. This suggests genuine reasoning rather than mere retrieval. That said, determining where learning ends and retrieval begins is philosophically complex.

What limitations does AI have in mathematical problem-solving?

AI still struggles with problems requiring conceptual breakthroughs—genuinely new frameworks or ways of thinking. It works best on problems with straightforward solutions amenable to systematic exploration. AI also can't always explain why its approach works in intuitive human terms. Additionally, verifying AI solutions still requires human expertise, and AI's reasoning is bounded by computational constraints. For the hardest, most novel problems in mathematics, human insight remains essential.

Will AI replace human mathematicians?

No. What's happening is more subtle: AI is becoming a research tool that augments human mathematicians. Humans provide insight and direction. AI provides systematic reasoning power and breadth of knowledge. The most effective approach combines both. In fact, elite mathematicians are increasingly using these tools, not being displaced by them. The skill set is shifting from "solve this problem" to "direct AI tools effectively," but the value of mathematical insight remains fundamental.

How does this change the field of mathematics going forward?

Several things will likely change: research will accelerate as AI handles systematic exploration, formalization may become standard practice rather than rare, the "long tail" of neglected problems might get solved faster, and human mathematicians will focus increasingly on conceptual breakthroughs and problem direction rather than routine problem-solving. New problems will emerge as old ones get solved. The interaction between humans and AI will define the frontier of mathematical knowledge.

What's the significance of Terence Tao's analysis?

Terence Tao is arguably the world's most influential active pure mathematician. His documentation of AI progress on Erdős problems—identifying eight cases of autonomous progress and six of accelerated progress—provides authoritative validation that this is real progress, not hype. His insight that AI is "better suited for being systematically applied to the long tail of obscure Erdős problems" because of scalability is particularly important. When a Fields Medalist endorses AI tools for mathematics, that carries weight throughout the mathematical community.

How can researchers start using AI for mathematical work?

Start with tools already available: use Chat GPT or Claude with extended thinking enabled for exploring mathematical problems and literature reviews. For formalization, learn Lean if you want to formally verify proofs. Consider specialized tools like Harmonic's Aristotle for automating formalization. Most importantly, view these tools as thinking partners that complement human insight, not replacements for mathematical understanding. Always verify AI-generated proofs independently.

Key Takeaways

• AI breakthrough in mathematics is real: 15 Erdős problems solved in weeks with 73% involving AI, not hype or cherry-picked examples
• Extended thinking changes everything: GPT 5.2's ability to spend computational resources on deep problem exploration dramatically improves mathematical reasoning
• Formalization is the gatekeeper: Automated verification tools like Lean and Aristotle make AI-generated mathematics trustworthy and verifiable
• Elite mathematicians are on board: When prestigious researchers publicly credit AI tools, that signals genuine utility beyond academic interest
• Human-AI teams are optimal: The best results combine human insight with machine reasoning power, not one replacing the other
• Scalability matters most: AI excels at systematically exploring the "long tail" of obscure problems that humans neglect because they're low-priority
• This changes research workflows: Literature review, problem exploration, proof verification, and formalization are all accelerated
• The frontier remains open: While AI tackles routine problems, genuinely novel breakthroughs still require human creativity and insight

Related Articles

• Prompt Repetition Boosts LLM Accuracy by 76%: The Technique Explained [2025]