How AI Is Cracking Unsolved Math Problems: The Axiom Breakthrough [2025]

How AI Is Finally Cracking Unsolved Math Problems

For five years, mathematicians Dawei Chen and Quentin Gendron were stuck. They'd been wrestling with a gnarly problem in algebraic geometry involving differentials—those elements of calculus that measure distance along curved surfaces. Their argument kept hitting the same wall: a strange formula from number theory that nobody could solve or justify. So they did what mathematicians do when they hit a dead end. They wrote it up as a conjecture instead of a theorem, published it, and moved on.

Then something shifted.

Chen spent hours trying to get Chat GPT to crack the problem. Nothing. The general-purpose AI models weren't equipped for this kind of deep mathematical reasoning. But at a math conference in Washington, DC last month, Chen ran into Ken Ono, a legendary mathematician who'd recently left the University of Virginia to join Axiom, an AI startup founded by one of his former students, Carina Hong.

Chen mentioned the problem. Casual conversation. The next morning, Ono walked up with something that changed everything: a complete proof, generated by Axiom's AI system called Axiom Prover.

This isn't hype. The proof is real. It's been posted to arXiv, the preprint repository where mathematicians share their work. And the AI didn't just fill in a missing piece—it found a connection that human mathematicians had completely missed, linking the problem to a numerical phenomenon from 19th-century mathematics that nobody had thought to apply.

What's happening at Axiom right now is a watershed moment for AI. Not because Axiom Prover has solved the most famous unsolved problems in mathematics (it hasn't—no Millennium Prize Problems yet). But because it's doing something that was considered impossible just a few years ago: genuinely assisting professional mathematicians on real research problems, verifying proofs with absolute certainty, and discovering novel solutions that humans missed.

This is different from Chat GPT making up citations or Copilot hallucinating code. This is AI producing mathematically rigorous, verifiable results that can advance human knowledge. And it's happening right now.

The Problem With Traditional AI and Mathematics

Here's the thing about large language models and math: they're terrible at it.

Well, not terrible exactly. Chat GPT can solve basic algebra problems. It can work through arithmetic. But ask it to prove something, really prove it, and things fall apart fast. The AI will confidently walk you through steps that seem right but don't actually hold up under scrutiny. It invents theorems that sound plausible. It misses logical connections. It gets stuck.

The fundamental issue is that language models are pattern-matching machines. They've been trained on text, and they're very good at predicting what word comes next based on statistical patterns. Math, especially at the research level, isn't about patterns. It's about logical necessity. A proof either works or it doesn't. There's no middle ground. There's no "close enough."

When you ask Chat GPT to prove something, it doesn't actually prove it. It generates text that looks like a proof because it's seen many proofs in its training data. But it's not following logical chains. It's not checking whether each step actually follows from the previous one. It's just predicting tokens.

This is why mathematicians have been skeptical of AI for years. They've watched the hype cycle. They've seen the breathless announcements. And they've tried the tools themselves and found them wanting.

The gap between general intelligence and mathematical reasoning is enormous. You can be brilliant at language and terrible at proofs. You can understand English perfectly and still not know whether a logical argument holds water. These are different cognitive domains.

Google Proof, a system that Google released in 2024, started closing that gap. But it was still limited. It could verify proofs that were already written. It could suggest next steps. But it wasn't generating genuinely novel solutions to unsolved problems. It was more of a helpful tool than a breakthrough.

Axiom's approach is different. And it's working.

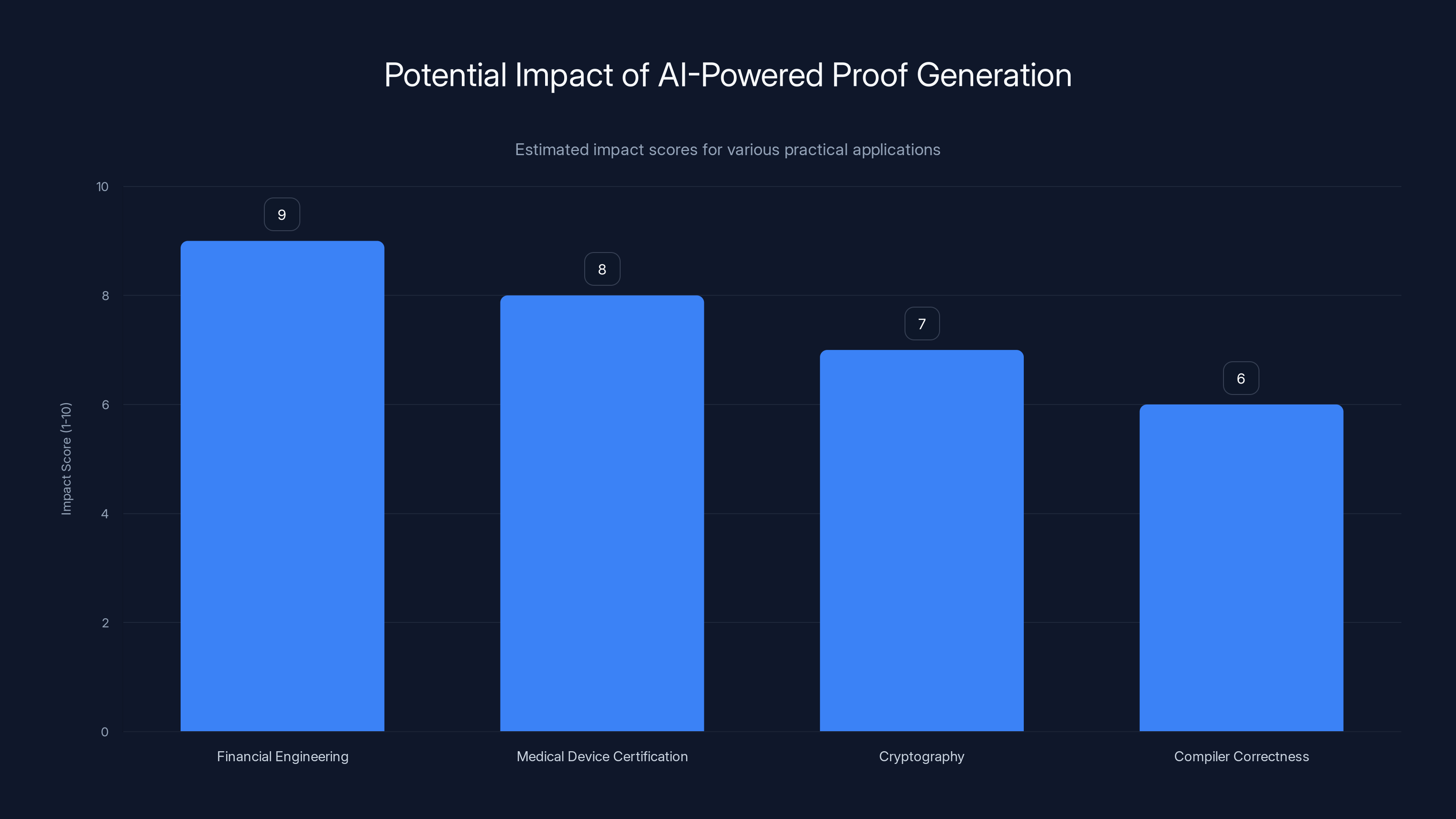
AI-powered proof generation could have the highest impact in financial engineering, followed by medical device certification, cryptography, and compiler correctness. Estimated data.

How Axiom Prover Actually Works

Axiom Prover isn't just a large language model with better prompting. It's a hybrid system that combines multiple AI approaches into something more powerful than either alone.

At its core, Axiom is using a large language model—probably something like GPT-4 or a similar frontier model—to generate candidate solutions. The LLM is good at making creative leaps, exploring different approaches, suggesting connections between ideas. But here's where it gets interesting: the LLM is working within constraints.

Those constraints come from Lean, a specialized mathematical language designed specifically for formal proof verification. Lean is not Python. It's not pseudocode. It's a formal language where every symbol has precise meaning and every statement can be checked for logical correctness by a machine.

When you write a proof in Lean, the system verifies every step. It checks that conclusions actually follow from premises. It confirms that you're using theorems correctly. It catches errors that a human might miss. It's like a mathematical proof with an automated referee that can't be fooled.

Here's how Axiom Prover works in practice:

1. The LLM generates potential proof strategies, approaches, and mathematical insights
2. The system attempts to formalize these ideas into Lean
3. The Lean verifier checks whether the proof is logically sound
4. If it works, you have a verified proof. If it doesn't, the system learns and tries again
5. The LLM can see what worked and what failed, and uses that feedback to generate better ideas

This feedback loop is crucial. The LLM isn't guessing blindly. It's getting real-time feedback about which approaches are mathematically valid. Over many iterations, this teaches the system to generate mathematically sensible ideas rather than plausible-sounding nonsense.

It's not a perfect system. It's not magic. But it's a genuinely new approach to combining AI creativity with mathematical rigor. And it's working.

The Chen-Gendron proof is one example. But Axiom has generated several others in recent weeks. Let's look at what else they've solved.

The Chen-Gendron Conjecture: AI Finding Hidden Connections

The problem Chen and Gendron had been stuck on involved something called differentials in algebraic geometry. If you remember calculus, you know that differentials measure infinitesimal changes. In algebraic geometry, this becomes more abstract. You're not just measuring change on a curve. You're measuring change in abstract algebraic spaces.

Their proof kept running into a formula from number theory that they couldn't justify. It was like having all the pieces of a puzzle except for one crucial connector. The formula was real—they could see it in the literature. But they couldn't prove why it should work for their specific problem.

What Axiom Prover did was remarkable: it found a bridge. It connected their algebraic geometry problem to a numerical phenomenon that had been studied in the 19th century. This phenomenon, which mathematicians had understood for more than a hundred years, turned out to be exactly what was needed to justify the formula.

This is the kind of insight that makes mathematicians go "oh, of course!" after you point it out. But finding it? That requires either years of background knowledge combined with creative thinking, or luck. The AI found it algorithmically.

Ken Ono, who presented the proof to Chen, describes the significance this way: "What Axiom Prover found was something that all the humans had missed." This is not a minor insight. This is a professional mathematician—one of the best in the field—saying that the AI made a genuine contribution to human knowledge.

The practical impact is immediate. Chen was able to turn his conjecture into a theorem. His work can now be published not as speculation but as established fact. For his research program, this is the difference between a promising idea and actual progress.

But the Chen-Gendron proof is just one of several recent breakthroughs. Another might be even more impressive.

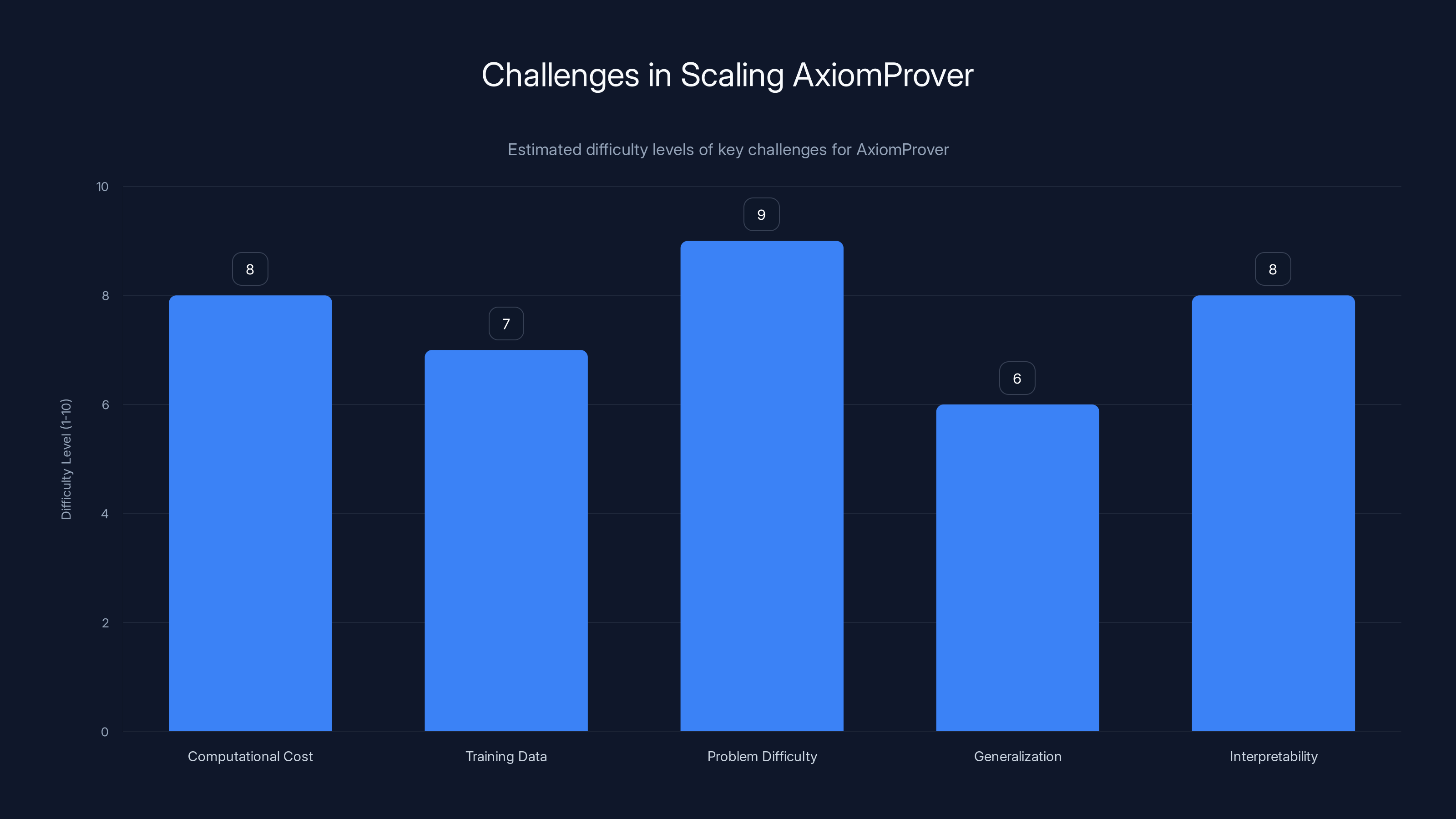
The chart estimates the difficulty of various challenges AxiomProver faces in scaling. Problem difficulty and interpretability are among the highest challenges. Estimated data.

Fei's Conjecture: Full Automation and Elegance

Fei's Conjecture concerns something called syzygies—mathematical expressions where numbers line up in specific patterns in algebra. The conjecture involves formulas that first appeared in the notebook of Srinivasa Ramanujan, the legendary Indian mathematician, more than 100 years ago.

Ramanujan was a mathematical genius who worked in the early 20th century. He discovered patterns and relationships in number theory that took other mathematicians decades to fully understand. His notebooks are still being mined for insights. Some of the problems he noted have never been solved.

Fei's Conjecture connects to this rich history. It's not a trivial problem. It's not a problem that's been sitting unsolved for a year or two. This is a conjecture that's been lurking in the mathematical literature, connected to the work of one of history's most famous mathematicians.

And Axiom Prover solved it. Completely. From start to finish.

This is different from the Chen-Gendron situation, where the AI helped bridge the gap in an argument that humans had mostly constructed. In Fei's Conjecture, the AI didn't have an almost-finished proof waiting in the wings. It generated the proof, original and complete, from first principles.

Scott Kominers, a professor at Harvard Business School who studies this kind of AI application and is familiar with both Fei's Conjecture and Axiom's technology, said something that captures the significance: "Even as someone who's been watching the evolution of AI math tools closely for years, and working with them myself, I find this pretty astounding. It's not just that Axiom Prover managed to solve a problem like this fully automated, and instantly verified, which on its own is amazing, but also the elegance and beauty of the math it produced."

This is important. Kominers isn't just saying the proof is correct. He's saying it's elegant. In mathematics, elegance matters. A proof that's correct but convoluted might verify logically but fail intellectually. A proof that's elegant reveals something about why the theorem is true, not just that it's true.

The fact that Axiom Prover generated elegant proofs suggests something deeper: the AI isn't just shuffling symbols. It's developing actual mathematical insight.

The Two Other Problems and What They Reveal

Axiom has also generated proofs for two additional unsolved problems. The third involves a probabilistic model related to "dead ends" in number theory—situations where certain mathematical approaches hit fundamental obstacles. The fourth draws on mathematical tools originally developed to solve Fermat's Last Theorem, one of the most famous problems in the history of mathematics.

Fermat's Last Theorem states that there are no three positive integers x, y, and z that can satisfy the equation (x^n + y^n = z^n) for any integer value of n greater than 2. This was conjectured in 1637 and not proven until 1995—a gap of 358 years. The proof, when it finally came, was revolutionary. It connected Fermat's problem to entirely different areas of mathematics, showing that the answer depended on understanding deep properties of elliptic curves.

The fact that Axiom Prover is leveraging techniques from Fermat's proof to solve new problems shows something important: the AI isn't just applying rigid formulas. It's picking up on mathematical strategies and knowing when to apply them to new situations.

What makes these four proofs collectively significant is the diversity. They span different areas of mathematics. They use different techniques. Some are fully automated, others build on human-generated partial proofs. Together, they show that Axiom Prover isn't just a one-trick system that works on one specific type of problem. It's a general mathematical reasoning engine.

But here's what's crucial to understand: Axiom hasn't solved any of the most famous unsolved problems yet. No Riemann Hypothesis. No P vs NP. No Yang-Mills Theory gaps. No problems from the Millennium Prize list.

But the direction is clear. And it's accelerating.

Why This Matters Beyond Pure Mathematics

Mathematicians might be excited about proofs for their own sake. But Axiom's CEO Carina Hong is thinking bigger.

"Math is really the great test ground and sandbox for reality," Hong says. "We do believe that there are a lot of pretty important use cases of high commercial value."

She's right. The techniques being developed here have applications far beyond academic mathematics.

Consider cybersecurity. Software vulnerabilities cost companies billions every year. Most security testing is empirical: you run the code, you test it in different scenarios, you try to break it. But empirical testing can never be exhaustive. There are always edge cases you missed.

Formal verification is different. It's a mathematical approach to proving that code will behave correctly under all possible conditions. You write a formal specification of what the code is supposed to do, and then you prove that the code actually does it. If the proof succeeds, you know with absolute certainty that the code is correct. Not probably correct. Certainly correct.

The problem with formal verification today is that it's expensive and time-consuming. Only the most critical systems get formally verified. A nuclear power plant control system? Yes. A standard web application? Almost never. It's too much work.

Now imagine if Axiom Prover could generate formal proofs of software correctness automatically. Imagine if you could take a code function and ask the AI to prove that it does what it's supposed to do. The economic impact would be enormous.

Beyond cybersecurity, similar logic applies to other fields:

Hardware design: Processors contain billions of transistors. Getting them right matters enormously. Intel's Pentium had a division bug in 1994 that cost the company hundreds of millions of dollars. Formal verification could prevent these catastrophic errors, and AI-assisted proof generation could make it practical to verify complex hardware designs.

Distributed systems: Modern software relies on distributed systems—databases, message queues, consensus protocols. These are notoriously hard to get right. Bugs can cause data loss, corruption, or inconsistency. AI-powered formal verification could prove that a distributed system will maintain consistency even when components fail.

Protocol verification: Network protocols, cryptographic protocols, blockchain consensus mechanisms—these all need to be correct. A bug could expose millions of users to attacks. Mathematical verification would provide absolute assurance.

Autonomous systems: Self-driving cars, drones, robots—these systems make decisions in the physical world. You can't afford edge case bugs. Formal verification could prove that an autonomous system will behave safely under all possible conditions.

These applications don't require solving the most famous unsolved problems in mathematics. They just require good mathematical reasoning, proof generation, and verification. This is exactly what Axiom is building.

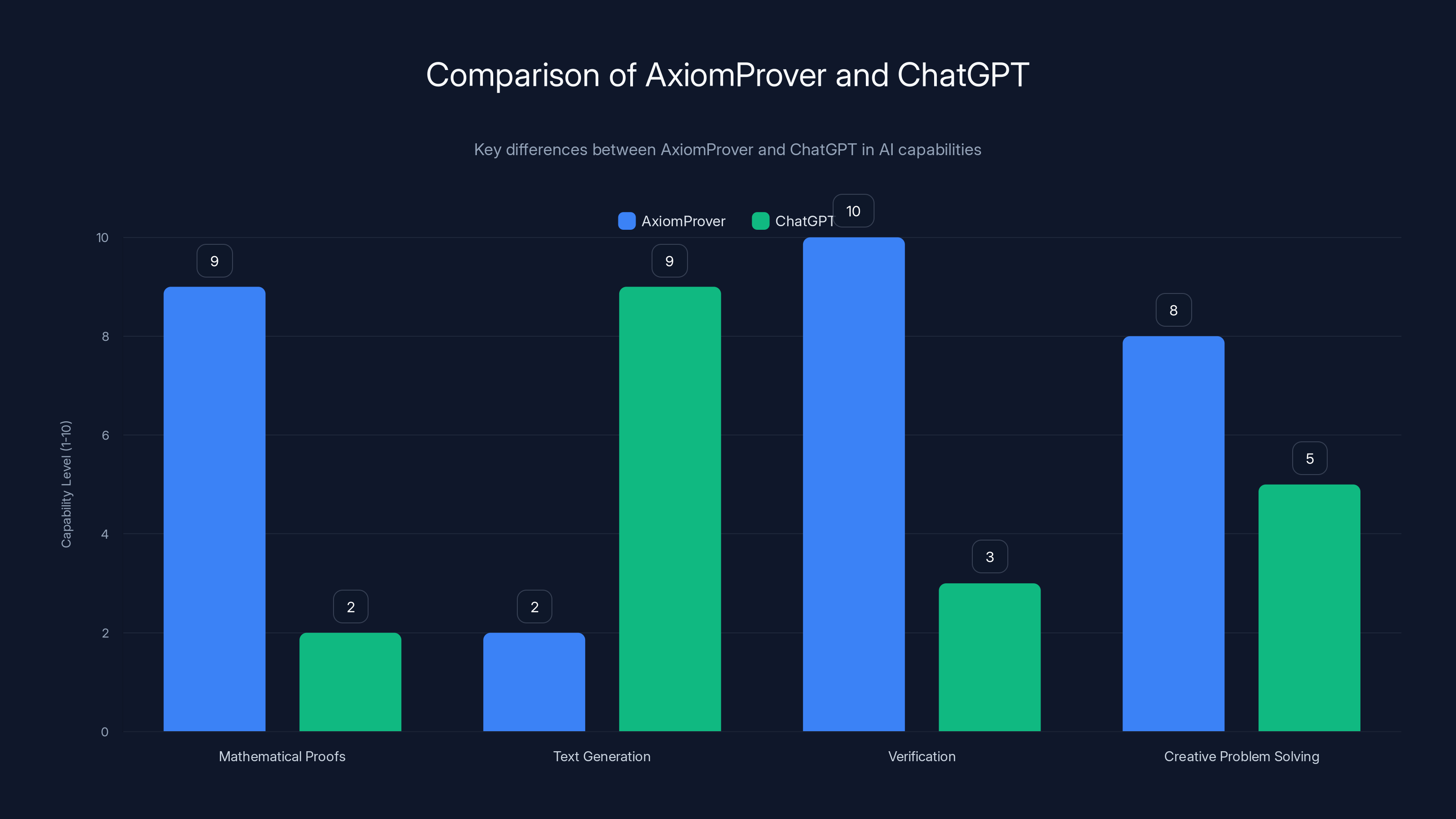
AxiomProver excels in generating and verifying mathematical proofs, while ChatGPT is stronger in general text generation. Estimated data based on described capabilities.

The Broader Context: Recent AI Advances in Reasoning

Axiom isn't operating in a vacuum. There's been a noticeable shift in AI over the past year toward systems that focus on reasoning rather than just language generation.

Google released Alpha Proof in 2024, which competed in the International Mathematical Olympiad. It didn't solve every problem, but it solved some of the hardest problems that elite high school mathematicians face. That's a different level from what frontier LLMs could do.

Open AI has been working on reasoning-focused models. There are indications that their newer systems have significantly improved mathematical abilities compared to earlier versions.

Anthropic, which makes Claude, has emphasized that their models are getting better at multi-step reasoning.

What's happening is a fundamental shift in how AI systems are built. For years, the focus was on scale—making models bigger, training on more data. The assumption was that scaling alone would solve everything. And it did help.

But there's a realization settling in: pure scale has limits. You can make a model that's great at predicting text, but that doesn't automatically make it great at logical reasoning. You need different architectures, different training approaches, different evaluation methods.

The hybrid approach that Axiom is using—combining LLMs for creative generation with formal systems for verification—is becoming a pattern. It's not just LLMs anymore. It's LLMs plus specialized reasoning engines. LLMs plus constraint solvers. LLMs plus verification systems.

This is a maturation of the field. And it's working.

What Mathematicians Actually Think

Ken Ono's perspective is especially revealing because he's not just using Axiom's system. He helped create it. And he's an active research mathematician, not just an entrepreneur trying to sell a product.

Ono tells WIRED that Axiom Prover demonstrates "a new paradigm for proving theorems." That's a significant claim. He's not saying it's a useful tool. He's saying it's a new way of doing mathematics entirely.

He's also interested in using Axiom Prover to understand something deeper: how mathematical discovery happens. "I'm interested in trying to understand if you can make these aha moments predictable," Ono says. "And I'm learning a lot about how I proved some of my own theorems."

This is fascinating. By studying how Axiom Prover generates proofs, Ono is gaining insights into his own mathematical thinking. The AI is becoming a tool for self-understanding as well as problem-solving.

Dawei Chen, the mathematician whose conjecture got solved, is also optimistic but measured: "Mathematicians did not forget multiplication tables after the invention of the calculator. I believe AI will serve as a novel intelligent tool—or perhaps an 'intelligent partner' is more apt—opening up richer and broader horizons for mathematical research."

This is important framing. Chen is saying the AI isn't going to replace mathematicians. It's going to extend them. The same way calculators didn't make mathematicians irrelevant—they freed mathematicians from arithmetic tedium so they could think about bigger problems.

When the AI can handle the mechanical parts of proof generation and verification, mathematicians can focus on intuition, on making creative leaps, on asking the right questions. The AI becomes a partner, not a replacement.

The Technical Innovation: Lean and Formal Verification

Underlying all of this is a technical choice: using Lean as the formal verification language.

Lean is a proof assistant. It's a programming language specifically designed to write mathematical proofs in a way that a computer can verify them. When you write a proof in Lean, every statement is checked. Every application of a theorem is verified. Every logical step is validated.

This is fundamentally different from writing proofs in English, even very carefully. In English, you might write "by the intermediate value theorem, there exists a point where..." A human reader understands this. But a computer would need to check: Is the function continuous? Is the interval bounded? Does the intermediate value theorem actually apply here?

In Lean, all of that has to be explicit. You can't wave your hand and say "obviously." You have to prove it.

This makes Lean proofs more laborious to write. You can't be as informal. But it also makes them absolutely airtight. If a Lean proof compiles, it's correct. Not probably correct. Certainly correct.

Axiom Prover uses Lean as a target language. The LLM generates proof ideas, and then those ideas are translated into Lean code. The Lean compiler verifies them. This combination is powerful: the LLM gets to be creative, and Lean gets to be certain.

Several major mathematicians have been embracing Lean in recent years. In 2021, a group of mathematicians led by Tom Hales started formalizing the proof of the Kepler conjecture—a famous problem about sphere packing. They chose Lean as their language. The project, called the Xena Project, has been steadily building a library of formalized mathematics.

The existence of this Lean library is important for Axiom. The more mathematics is formalized in Lean, the more patterns the AI can learn from, and the better it can become at generating valid proofs.

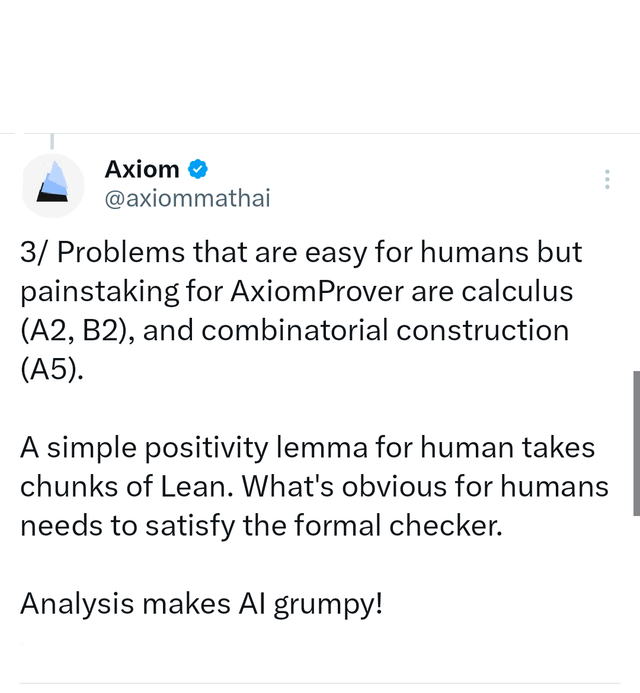
Estimated data shows that while the Lean verification stage has the lowest initial success rate, the feedback loop significantly improves overall process efficiency.

The Limitations and What Remains Unsolved

Let's be clear about what Axiom Prover hasn't done yet. It hasn't solved any of the most famous open problems. The Riemann Hypothesis remains unsolved. The P vs NP problem is untouched. Yang-Mills existence and the mass gap—still open. The Hodge conjecture, the Birch and Swinnerton-Dyer conjecture—all untouched.

These problems are harder. They're harder not just in the sense that they've been open longer, but in the sense that attacking them requires deep insights that the AI probably hasn't developed yet.

The Riemann Hypothesis, for example, concerns the distribution of prime numbers. Mathematicians have been attacking it for almost 160 years. Countless approaches have been tried. Many have led nowhere. To solve it, you'd probably need a genuinely novel insight—something that's never occurred to any human mathematician in all that time.

Can AI generate such an insight? Maybe. But we don't know yet. The system would need to explore vast mathematical space, develop intuitions about what's likely to be fruitful, and have the kind of persistent insight that human mathematical genius develops over years of immersion in a problem.

Axiom Prover might be able to do this. But it hasn't yet. These are aspirational targets, not accomplished facts.

There's also the question of what "solving" a problem means. Some unsolved problems are asking for a proof of a statement. Others are asking for a proof that something is impossible. Still others are asking for an algorithm or a characterization. The types of mathematical reasoning required vary widely.

Axiom Prover has shown strength on some types of problems but hasn't been tested comprehensively across all types.

Practical Applications: Where This Gets Real

While the mathematical breakthroughs are impressive, the real value might be in applications. Let's think through some scenarios where AI-powered proof generation could actually be transformative.

Scenario 1: Financial engineering. Banks and hedge funds rely on mathematical models. These models involve complex stochastic calculus, differential equations, and statistical reasoning. When implemented in code, bugs can be catastrophic. A small error in a volatility calculation or a pricing model could lead to billions in losses. If a system like Axiom Prover could prove that a financial model is correctly implemented, that would be incredibly valuable.

Scenario 2: Medical device certification. Regulatory agencies like the FDA require that medical devices be safe. For devices that use algorithms or AI, proving safety is complex. If you could use AI-powered formal verification to prove that a diagnostic algorithm will classify patients correctly, or that a drug delivery system will administer the correct dose, that would accelerate development and increase confidence in safety.

Scenario 3: Cryptography. New cryptographic algorithms are proposed regularly. Some are secure. Some have subtle flaws. If you could use formal verification to prove that a cryptographic protocol is secure against known attacks, you'd have much more confidence in the protocol. This could accelerate the development of post-quantum cryptography, which is urgently needed as quantum computers advance.

Scenario 4: Compiler correctness. Programming languages have compilers that translate code into machine instructions. If there's a bug in the compiler, your code might not do what you intended. Some compilers have been formally verified, but it's expensive and slow. If AI could help verify compiler correctness, that would be significant.

None of these applications require solving the Riemann Hypothesis. They just require good mathematical reasoning applied to practical problems.

The Race for AI Mathematical Reasoning

Axiom isn't the only company or research group working on AI and mathematical reasoning. This has become a competitive area.

Google has Alpha Proof. They're clearly investing in this space. Their IMO performance suggests they have competent systems.

Meta (Facebook's parent company) has research groups working on theorem proving and mathematical reasoning.

Open AI presumably has internal research on mathematical reasoning, though they've been less public about it.

Chinese research groups have been active in this area as well. University of Science and Technology of China, for example, has been doing work on AI for mathematics.

This competitive dynamic will probably accelerate progress. If Axiom is showing impressive results, other labs will redouble their efforts. If one group achieves a breakthrough, others will work to match or exceed it.

Historically, competitive pressure in AI research has led to rapid improvements. We saw it with language models—once Chat GPT showed what was possible, everyone else rushed to catch up. We'll probably see the same thing with mathematical reasoning.

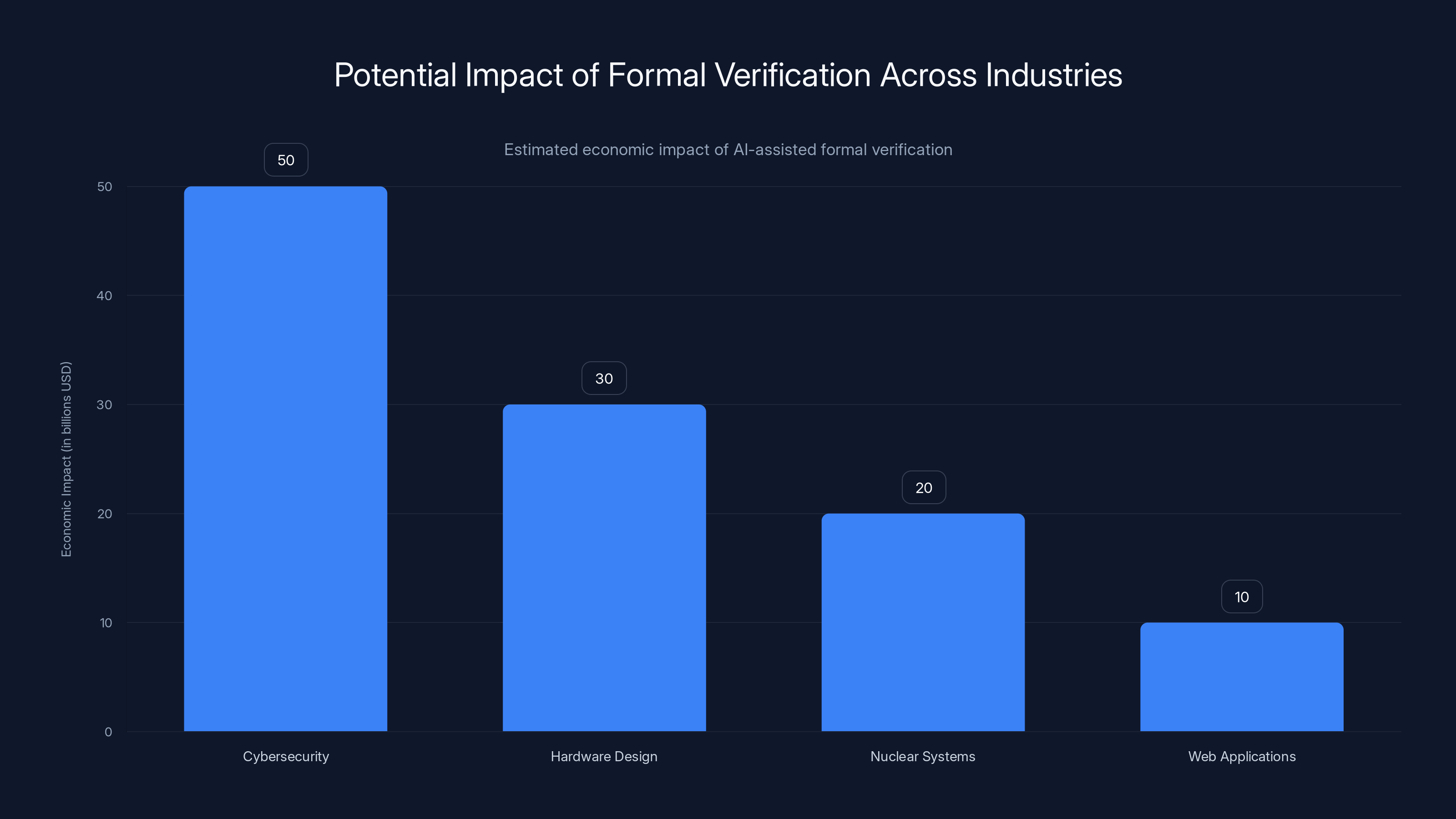
Estimated data suggests AI-assisted formal verification could save billions across various industries by preventing errors and enhancing security.

Sociological Implications: How This Changes Mathematics

If AI systems get significantly better at mathematical reasoning, it will change the culture of mathematics in subtle but important ways.

Right now, being a mathematician means developing deep expertise, spending years thinking about hard problems, building intuition through immersion. You become an expert by internalizing vast amounts of knowledge and developing pattern recognition.

If AI systems can do some of this work—can verify proofs, can suggest next steps, can generate candidate solutions—the role of the human mathematician changes.

It doesn't disappear. But it shifts. Instead of spending months on a detailed proof, a mathematician might spend days generating the right idea and then letting the AI handle the formalization and verification. The bottleneck moves from execution to conception.

This could be democratizing. Right now, to do cutting-edge mathematics, you typically need a Ph.D., access to a university, connections to a research community. If AI tools can lower the technical barriers, more people might be able to contribute to mathematical research.

Or it could be concentrating. If the best mathematicians are those who are best at directing AI systems, and if that's a skill that some people have and others don't, it could actually increase inequality within mathematics.

Most likely, it will be a mix. Some democratization, some concentration. The field will adapt and evolve.

Ken Ono's comment about learning more about how he himself proves theorems is insightful. By understanding how Axiom Prover works, mathematicians might develop a deeper understanding of mathematical reasoning itself. This could lead to new pedagogical approaches, new ways of teaching mathematics.

The Business Model Question

Here's something that's not entirely clear: how does Axiom make money?

Axiom is a private startup. They've presumably raised funding, but the business model isn't entirely obvious from the outside. Are they planning to sell access to Axiom Prover to mathematicians and researchers? Are they planning to license the technology to other companies for applications like formal verification? Are they planning to eventually be acquired by a larger tech company?

Carina Hong has mentioned that there are "high commercial value" use cases, suggesting they're thinking about practical applications, not just academic recognition.

The most likely scenarios are:

1. B2B licensing to tech companies for formal verification and safety-critical systems
2. API access for researchers willing to pay for improved mathematical capabilities
3. Acquisition by a larger AI company or tech company wanting this capability
4. Government contracts for applications in defense, aerospace, or other sensitive areas

Each of these could be lucrative. Formal verification for safety-critical systems is a multi-billion dollar market. If Axiom can make formal verification practical and affordable through AI, that's enormous.

The academic mathematics use case is probably smaller commercially, but it's valuable for credibility and for attracting talent. The fact that they're publishing proofs and working with academic mathematicians gives them visibility and reputation.

It's a smart strategy: build credibility through academic results, then monetize through practical applications.

What's Next: Scaling and Challenges

Axiom has proven the concept works. Axiom Prover can generate novel proofs to unsolved problems. The next question is: how much further can this scale?

There are several challenges to overcome:

Computational cost: Generating proofs requires running the LLM many times, trying different approaches, exploring possibilities. This is computationally expensive. As problems get harder, the cost might increase. Can Axiom scale this up efficiently?

Training data: Most of the mathematics that's been done is not formalized in Lean. It's written in English or informal notation. Building a larger library of formalized mathematics would help, but it's labor-intensive.

Problem difficulty: The problems Axiom Prover has solved so far are hard but not at the very frontier of mathematical difficulty. Can it tackle problems that have stumped the best mathematicians for decades?

Generalization: Axiom Prover has shown strength across different types of problems, but there are areas of mathematics where it hasn't been tested. How well does it generalize to entirely new domains?

Interpretability: When Axiom Prover generates a proof, mathematicians can understand it and verify it. But they might not understand why the AI chose that particular approach. As proofs get more complex, this interpretability question becomes more important.

These are solvable challenges, not fundamental obstacles. But they'll require continued research and development.

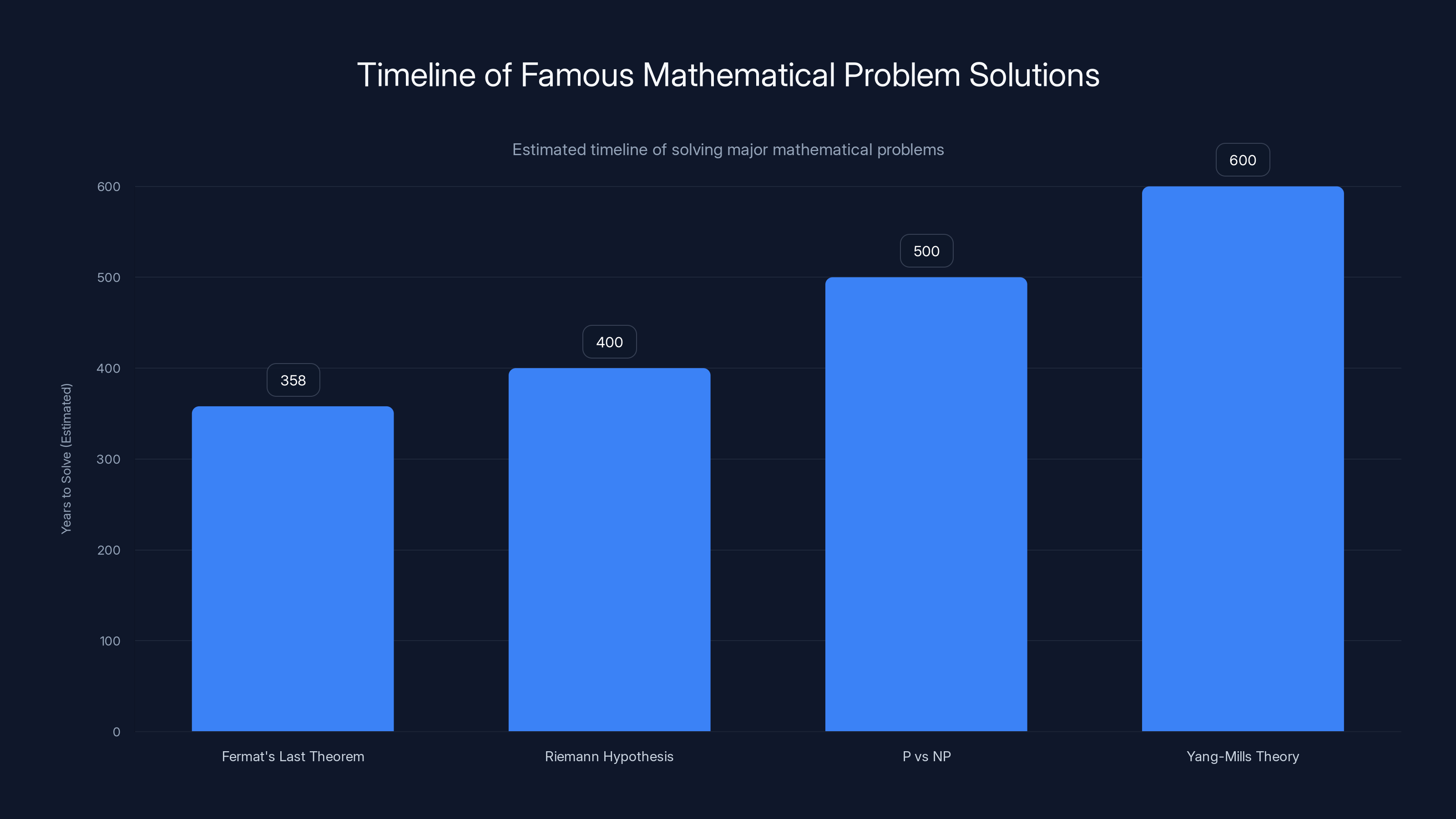
Estimated data suggests that while Fermat's Last Theorem took 358 years to solve, other major problems like the Riemann Hypothesis and P vs NP might take even longer. Estimated data.

The Historical Moment: Why This Matters

Step back and think about the big picture for a moment.

For most of human history, mathematics was the domain of individual genius. There was no way to systematize mathematical thinking. You had to be smart, study hard, develop intuition, have insights. The greats—Euler, Gauss, Riemann, Ramanujan—were remembered because they had minds that worked in ways others couldn't replicate.

Then in the 20th century, we started formalizing mathematics. We developed logic systems, set theory, proof theory. We realized that mathematical reasoning could be written down precisely. This led to computers being applied to mathematics.

But for decades, the computer's role was limited. Computers could compute. They could check special cases. They couldn't reason.

Now we're at a moment where computers might be able to reason mathematically. Not perfectly, not on the hardest problems, but meaningfully.

This is a fundamental shift in human capability. It's not quite as historically momentous as the development of mathematical reasoning itself, but it's substantial.

It means that mathematical discovery is no longer purely a human endeavor. It's a partnership between human mathematicians and AI systems.

We're not sure yet how far this partnership can go. We don't know if AI will eventually solve the great open problems. We don't know if AI will reveal entirely new domains of mathematics. We don't know if the creative insights that human mathematicians value most will ever emerge from AI systems.

But we know it's possible. And we're starting to see it in practice.

Expert Perspectives: What Researchers Are Saying

Beyond Ken Ono and Scott Kominers, the mathematical community is watching this closely. Some researchers have been enthusiastic early adopters of AI tools for mathematics. Others are skeptical.

The skepticism is healthy. Extraordinary claims require extraordinary evidence. The field has seen hype before. But the skepticism is softening as the evidence accumulates.

One thing that researchers emphasize is the importance of verification. The fact that Axiom Prover's proofs can be verified in Lean is crucial. This isn't a black-box system that claims to have solved a problem. It's generating proofs that can be independently checked. This is how mathematical progress has always worked: you make a claim, others verify it, and only then is it accepted as fact.

The other thing researchers emphasize is collaboration. The most interesting mathematical results are coming from humans and AI working together, not from AI alone. The human mathematician provides the intuition and direction. The AI provides the computational power and verification. Together, they achieve more than either could alone.

This collaborative model is probably going to be the future, at least for the foreseeable future. Not "AI replaces mathematicians" but "mathematicians and AI work together."

Misconceptions to Avoid

There's a lot of hype around AI and mathematics right now. Let's clear up some misconceptions:

Misconception 1: Axiom Prover is just Chat GPT with better prompting. No. It's a completely different system that combines LLMs with specialized reasoning engines and formal verification. The architecture is fundamentally different.

Misconception 2: Axiom Prover has solved hard problems like the Riemann Hypothesis. No. It's solved some important unsolved problems, but not the most famous ones. And many of the most famous problems remain unsolved.

Misconception 3: This means mathematicians will soon be obsolete. No. If anything, it means good mathematicians will become more valuable. The bottleneck shifts from execution to conception. Creative insight, problem selection, and mathematical intuition remain distinctly human skills.

Misconception 4: This technology is ready for widespread deployment. Not yet. It's still experimental. It works for some types of problems but not others. The computational cost is high. The system is still being developed and refined.

Misconception 5: This is purely academic with no practical applications. Not at all. The formal verification applications alone could be worth billions if executed well.

Looking Forward: The Next Five Years

If Axiom continues to progress at the current rate, what might we see in the next five years?

Optimistically: Axiom Prover becomes a standard tool in mathematics research. Dozens of major unsolved problems get solved. Several of the Millennium Prize Problems fall. AI-powered formal verification becomes standard practice in critical systems. The business is valued at billions.

Realistically: Axiom Prover solves more unsolved problems but doesn't crack the most famous ones. It becomes a useful tool for a subset of mathematicians. Formal verification adoption accelerates but doesn't become universal. The business succeeds but doesn't become enormous.

Pessimistically: Progress stalls. The problems get harder faster than the tools improve. Computational costs become prohibitive. The hype exceeds the reality and the field backlashes.

Most likely, reality will be somewhere between realistic and optimistic. Significant progress, but not transformation. Axiom might not become a household name, but its impact on mathematics will be real.

The mathematical community is watching. Younger mathematicians are especially interested in these tools. Over time, as new mathematicians are trained in a world where AI assistance is normal, the culture of mathematics will shift.

And that shift might be just as important as the specific theorems solved.

The Broader Vision: Mathematics as Scaffold

Carina Hong's comment about mathematics being "the great test ground and sandbox for reality" points to something deeper than just solving math problems.

Mathematics is abstract. It's formal. It's precise. In some sense, it's the easiest domain for AI to work in because there are clear rules, clear definitions, clear standards for correctness.

If AI can master mathematics, if it can develop genuine reasoning ability in such a rigorous domain, that's evidence that AI could potentially develop reasoning ability in other domains too.

The techniques being developed for mathematical reasoning—the hybrid LLM plus formal verification approach, the iterative refinement loop, the feedback mechanisms—might be applicable to other fields. Not medicine, not law, not engineering—at least not immediately. But eventually, perhaps.

So in a sense, Axiom's work on mathematical reasoning is pioneering approaches that might eventually be applied much more broadly. Mathematics isn't the final destination. It's the laboratory where we learn how to build systems that can reason.

This is why the broader AI research community is watching Axiom closely. Not just because they care about mathematics, but because what Axiom is learning might be relevant to the future of AI reasoning in general.

Conclusion: A New Chapter in Mathematics

Dawei Chen's conjecture is solved. Fei's Conjecture is solved. Several other unsolved problems are solved. And these aren't trivial mathematical curiosities. These are problems that real mathematicians have spent years thinking about. Problems that connect to deep mathematical structures. Problems that represent genuine contributions to human knowledge.

And they were solved by an AI system that's less than a year old.

That's significant. Not earth-shattering, but significant.

It means we've entered a new chapter in mathematics. A chapter where artificial intelligence isn't just a tool for computation or for searching literature. It's a tool for reasoning, for generating insights, for discovering proofs.

It doesn't mean mathematicians are obsolete. If anything, it means good mathematicians will be more in demand than ever. The machines can handle the mechanical parts. What humans bring—intuition, creativity, the ability to ask the right question—becomes more valuable.

Ken Ono describes Axiom Prover as a "new paradigm for proving theorems." That might be the most important takeaway. This isn't an incremental improvement to existing methods. It's a different approach to mathematical reasoning. And the early results suggest it works.

Where does this go? We don't know yet. But we're about to find out. The next few years of mathematical research will tell us whether this is a genuine breakthrough or an impressive proof of concept that hits diminishing returns.

Either way, something has shifted. The partnership between human mathematicians and artificial intelligence has started. And it's already producing results.

FAQ

What is Axiom Prover and how is it different from Chat GPT?

Axiom Prover is a specialized AI system developed by Axiom that combines large language models with formal verification in a language called Lean. Unlike Chat GPT, which generates text based on statistical patterns, Axiom Prover generates mathematical proofs that are automatically verified for logical correctness. Every step in an Axiom Prover proof is checked by the Lean verifier to ensure absolute mathematical certainty, making it fundamentally different from general-purpose language models that can produce confident-sounding but incorrect statements.

How does AI actually solve math problems that humans couldn't?

Axiom Prover works through a feedback loop: the AI generates candidate proof strategies, attempts to formalize them in Lean, receives verification results from the Lean compiler, and uses that feedback to generate better ideas. It doesn't solve problems through magical reasoning but through systematic exploration combined with pattern recognition learned from formalized mathematics. In the case of Chen and Gendron's conjecture, the AI found a connection to 19th-century number theory that human mathematicians had overlooked, suggesting the system can make creative leaps that require vast knowledge synthesis.

What are the practical applications of this AI math breakthrough?

Beyond academic mathematics, AI-powered mathematical reasoning has significant applications in formal verification of software, which is critical for cybersecurity, medical devices, autonomous systems, and financial software. If Axiom Prover could automatically generate proofs that code is correct, it would be transformative for safety-critical systems. Other applications include proving cryptographic protocols are secure, verifying compiler correctness, and ensuring hardware designs are free from subtle bugs that might cause failures.

Can Axiom Prover solve famous unsolved problems like the Riemann Hypothesis?

Not yet. While Axiom Prover has solved several important unsolved problems, it hasn't tackled the most famous open problems in mathematics, such as the Riemann Hypothesis, P vs NP, or the Birch and Swinnerton-Dyer Conjecture. These problems likely require deeper insights that the system hasn't yet developed. However, the fact that Axiom Prover can solve some previously unsolved problems suggests it's on a trajectory toward tackling harder problems, though success is not guaranteed.

Will AI replace human mathematicians?

Unlikely. If anything, good mathematicians may become more valuable as AI handles mechanical aspects of proof generation and verification. The bottleneck in mathematics shifts from execution to conception, making the human ability to ask the right questions and develop intuition even more important. The collaborative model—humans providing direction and creativity, AI providing computational power and verification—appears to be the most productive approach.

How does Lean verification ensure Axiom Prover's proofs are actually correct?

Lean is a formal proof verification language where every logical step is checked by a computer. When you write a proof in Lean, you can't make informal arguments or skip steps. Every application of a theorem must be verified, every logical inference must be validated. If a Lean proof compiles successfully, it's guaranteed to be mathematically correct—not probably correct, but certainly correct. This automated verification eliminates the possibility of subtle errors that might slip through even carefully reviewed human proofs.

What does this mean for the future of AI reasoning in other fields?

Mathematics is serving as a laboratory for developing AI reasoning systems. The techniques being developed—combining language models with specialized reasoning engines and formal verification—might eventually apply to other domains requiring rigorous thinking. However, most other fields don't have the formal verification tools that mathematics has, so broader applications may take years to develop. Success in mathematical reasoning provides evidence that AI can develop genuine reasoning ability, not just pattern matching.

How much does it cost to use Axiom Prover?

Pricing information for Axiom Prover hasn't been widely published. As a startup, Axiom is likely still determining the optimal pricing model. Potential approaches include direct licensing to researchers, API access subscriptions, or enterprise licensing to companies needing formal verification. The company has indicated there are valuable commercial use cases, suggesting pricing will eventually support business applications rather than just academic research.

What makes mathematical reasoning harder for AI than generating text?

Mathematical reasoning requires logical necessity rather than statistical correlation. While language models excel at predicting what word comes next based on patterns, mathematics demands that each step must logically follow from previous steps. A proof either works or it doesn't—there's no middle ground. Additionally, mathematical creativity often requires combining insights from distant areas (as Axiom Prover did with 19th-century number theory), demanding knowledge synthesis across specialized domains that general language models struggle with.

How is Axiom funded and what's their business model?

Axiom is a private startup that has presumably raised venture capital funding. While specific business model details haven't been fully disclosed, CEO Carina Hong has mentioned valuable commercial use cases, suggesting the company plans to monetize through formal verification applications, licensing the technology to other companies, or eventually being acquired by a larger tech company. The academic work serves to build credibility and attract talent while the company develops commercial applications.

Key Takeaways

• AxiomProver solved 4 previously unsolved math problems by combining LLMs with formal verification in Lean, proving AI can now perform genuine mathematical reasoning beyond pattern matching
• The system works through a feedback loop where AI generates proof strategies, Lean verifies correctness, and failures inform better ideas—a fundamentally different approach from general-purpose ChatGPT
• Chen-Gendron conjecture proof found a hidden connection to 19th-century mathematics that expert human mathematicians had completely overlooked for years, demonstrating AI's potential for creative mathematical insights
• Practical applications extend far beyond academic mathematics to formal verification of critical software, cryptography, autonomous systems, and medical devices—potentially worth billions in economic value
• The future of mathematics will likely involve human-AI collaboration rather than replacement, with AI handling mechanical proof generation while humans focus on intuition, creativity, and problem selection

Related Articles

• Amazon Alexa+ Free on Prime: Full Review & Early User Warnings [2025]
• Nvidia's $100B OpenAI Gamble: What's Really Happening Behind Closed Doors [2025]
• Inside Moltbook: The AI-Only Social Network Where Reality Blurs [2025]
• OpenAI Staff Exodus: Why Senior Researchers Are Leaving 2025
• AI Agents Getting Creepy: The 5 Unsettling Moments on Moltbook [2025]
• SpaceX Acquires xAI: The 1 Million Satellite Gambit for AI Compute [2025]